
 如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )| A. | 15个 | B. | 14个 | C. | 13个 | D. | 12个 |
分析 首先过A作AE⊥BC,当D与E重合时,AD最短,首先利用等腰三角形的性质可得BE=EC,进而可得BE的长,利用勾股定理计算出AE长,然后可得AD的取值范围,进而可得答案.
解答  解:过A作AE⊥BC,
解:过A作AE⊥BC,
∵AB=AC,
∴EC=BE=$\frac{1}{2}$BC=12,
∴AE=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∵D是线段BC上的动点(不含端点B、C).
∴5≤AD<13,
∵线段AD长为正整数,
∴AD的可以有,15条,长为12,11,10,9,8,7,6,5,6,7,8,9,10,11,12,
∴点D的个数共有15个,
故选A.
点评 此题主要考查了等腰三角形的性质和勾股定理,关键是正确利用勾股定理计算出AD的最小值,然后求出AD的取值范围.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | k$≤\frac{9}{8}$ | B. | k$>\frac{9}{8}$ | C. | k$≤\frac{9}{8}$且k≠0 | D. | k$<\frac{9}{8}$且k≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
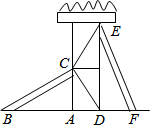 如图所示,有两个长度相同的滑梯BC和EF,CA⊥BF,ED⊥BF,垂足分别为A,D,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.问:两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
如图所示,有两个长度相同的滑梯BC和EF,CA⊥BF,ED⊥BF,垂足分别为A,D,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.问:两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2:3 | B. | 4:16 | C. | 3:2 | D. | 16:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 2 | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),直线m为横坐标都为2的点组成的一条直线,作出△ABC关于直线m对称的△A1B1C1,并直接写出A1,B1,C1的坐标.
如图所示,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),直线m为横坐标都为2的点组成的一条直线,作出△ABC关于直线m对称的△A1B1C1,并直接写出A1,B1,C1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
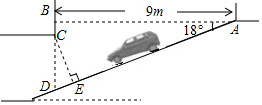 为缓解“停车难”的问题,某单位拟造地下停车库,建筑设计师提供了该地下停车库的设计示意图如图所示,已知该坡道的水平距离AB的长为9m,坡面AD与AB的夹角∠BAD=18°,石柱BC=0.5m,按规定,地下停车库坡道上方BC处要张贴限高标志,以便告知停车人车辆能否安全驶入.请你帮设计师计算一下CE的高度,以便张贴限高标志,结果精确到0.1m.
为缓解“停车难”的问题,某单位拟造地下停车库,建筑设计师提供了该地下停车库的设计示意图如图所示,已知该坡道的水平距离AB的长为9m,坡面AD与AB的夹角∠BAD=18°,石柱BC=0.5m,按规定,地下停车库坡道上方BC处要张贴限高标志,以便告知停车人车辆能否安全驶入.请你帮设计师计算一下CE的高度,以便张贴限高标志,结果精确到0.1m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com