
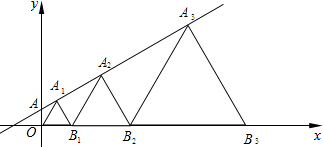
 如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )
如图,在直线y=$\frac{\sqrt{3}}{3}$x+1上取一点A1,以O、A1为顶点做第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样做下去,则第10个等边三角形的边长为( )| A. | ($\frac{\sqrt{3}}{3}$)9 | B. | ($\frac{\sqrt{3}}{3}$)10 | C. | 29•$\sqrt{3}$ | D. | 210•$\sqrt{3}$ |
分析 作A1D⊥x轴于D,A2E⊥x轴于E,根据等边三角形的性质得OD=B1D,B1E=B2E,∠OA1D=30°,∠B1A2E=30°,设OD=t,B1E=a,则A1D=$\sqrt{3}$t,A2E=$\sqrt{3}$a,则A1点坐标为(t,$\sqrt{3}$t),把A1(t,$\sqrt{3}$t)代入y=$\frac{\sqrt{3}}{3}$x+1可解得t=$\frac{\sqrt{3}}{2}$,于是得到B1点的坐标为($\sqrt{3}$,0),OB1=$\sqrt{3}$,则A2点坐标为($\sqrt{3}$+a,$\sqrt{3}$a),然后把A2($\sqrt{3}$+a,$\sqrt{3}$a)代入y=$\frac{\sqrt{3}}{3}$x+1可解得a=$\sqrt{3}$,B1B2=2$\sqrt{3}$,同理得到B2B3=4$\sqrt{3}$,…,按照此规律得到B9B10=29$\sqrt{3}$.
解答 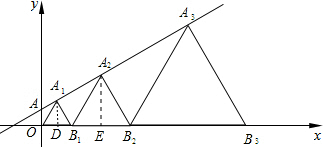 解:作A1D⊥x轴于D,A2E⊥x轴于E,如图,
解:作A1D⊥x轴于D,A2E⊥x轴于E,如图,
∵△OA1B1、△B1A2B2均为等边三角形,
∴OD=B1D,B1E=B2E,∠OA1D=30°,∠B1A2E=30°,
设OD=t,B1E=a,则A1D=$\sqrt{3}$t,A2E=$\sqrt{3}$a,
∴A1点坐标为(t,$\sqrt{3}$t),
把A1(t,$\sqrt{3}$t)代入y=$\frac{\sqrt{3}}{3}$x+1得$\sqrt{3}$t=$\frac{\sqrt{3}}{3}$t+1,解得t=$\frac{\sqrt{3}}{2}$,
∴OB1=$\sqrt{3}$,
∴A2点坐标为($\sqrt{3}$+a,$\sqrt{3}$a),
把A2($\sqrt{3}$+a,$\sqrt{3}$a)代入y=$\frac{\sqrt{3}}{3}$x+1得$\sqrt{3}$a=$\frac{\sqrt{3}}{3}$($\sqrt{3}$+a)+1,解得a=$\sqrt{3}$,
∴B1B2=2$\sqrt{3}$,
同理得到B2B3=22$\sqrt{3}$,…,按照此规律得到B9B10=29$\sqrt{3}$.
故选C.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线,直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了等边三角形的性质.


科目:初中数学 来源: 题型:解答题
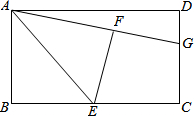 在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,猜想线段GF与GC有何数量关系?并证明你的结论.
在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,猜想线段GF与GC有何数量关系?并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
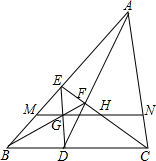 如图所示,已知D,E分别是△ABC的边BC,AB上的点,AD,CE交F,BF,DE交于G,过G作BC的平行线MN,交AB,CE,AC于M,H,N,求证:GH=NH.
如图所示,已知D,E分别是△ABC的边BC,AB上的点,AD,CE交F,BF,DE交于G,过G作BC的平行线MN,交AB,CE,AC于M,H,N,求证:GH=NH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
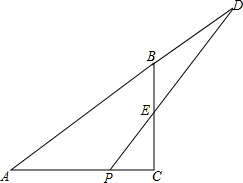 如图.在Rt△ABC中.∠ACB=90°,AB=10,BC:AC=3:4,点D在AB延长线上,BD=6,点P是AC上的-个动点.PD交BC于点E.设PC=x,S△PCE=y.
如图.在Rt△ABC中.∠ACB=90°,AB=10,BC:AC=3:4,点D在AB延长线上,BD=6,点P是AC上的-个动点.PD交BC于点E.设PC=x,S△PCE=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:已知AB是⊙O的直径,直线l与⊙O相切于点C,且弦CD⊥AB,垂足为E,BF⊥l,垂足为F,BF交⊙O于G.
如图:已知AB是⊙O的直径,直线l与⊙O相切于点C,且弦CD⊥AB,垂足为E,BF⊥l,垂足为F,BF交⊙O于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com