
分析 (1)原式中括号中利用平方差公式及完全平方公式化简,整理后利用多项式除以单项式法则计算得到最简结果,把a与b的值代入计算即可求出值;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a=$\sqrt{2}$代入计算即可求出值.
解答 解:(1)原式=(2a2-3ab-2b2-2a2+8ab-8b2)÷(5b)=(5ab-10b2)÷(5b)=a-2b,
当a=2,b=-1时,原式=2-2×(-1)=4;
(2)原式=$\frac{a+1-a+1}{(a+1)(a-1)}$•$\frac{2(a+1)(a-1)}{a}$=$\frac{4}{a}$,
由于a≠±1,
则当a=$\sqrt{2}$时,原式=2$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
| BC(单位:米) | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
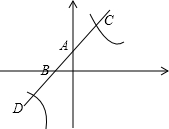 如图,直线y=x+n与坐标轴交于A,B两点,与反比例函数$y=\frac{k}{x}$的图象交于C,D两点,且BD•CB=6,则k=( )
如图,直线y=x+n与坐标轴交于A,B两点,与反比例函数$y=\frac{k}{x}$的图象交于C,D两点,且BD•CB=6,则k=( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 根据题意完成下列推理过程:
根据题意完成下列推理过程:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则ac>bc | B. | $\sqrt{a^2}$=a(a是实数) | ||
| C. | 三角形的三条中线相交于同一点 | D. | 内错角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
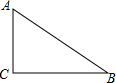 如图,在Rt△ABC中,∠ACB=90°.AC=3,cosB=$\frac{4}{5}$
如图,在Rt△ABC中,∠ACB=90°.AC=3,cosB=$\frac{4}{5}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com