
分析 根据题意,得出等号左边分母上的数比等号右边第一个分母上数大1,且这两个数分母上的数相乘等于最后一个数的分母,即可得出$\frac{1}{5}=\frac{1}{6}+\frac{1}{30}$,进而分析可得在$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,有(2+1)2=3+6;在$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,有(3+1)2=4+12,进而得出a+b的值.
解答 解:∵$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$;$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$;$\frac{1}{4}=\frac{1}{5}+\frac{1}{20}$=$\frac{1}{5}+\frac{1}{20}$,
∴$\frac{1}{5}=\frac{1}{6}+\frac{1}{30}$,
∵$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,有(2+1)2=3+6;$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,有(3+1)2=4+12;
∴如果理想分数$\frac{1}{n}$=$\frac{1}{a}$$+\frac{1}{b}$,那么a+b=(n+1)2.
故答案为:$\frac{1}{6}+\frac{1}{30}$;(n+1)2.
点评 本题主要考查了数字变化规律,培养学生通过观察、归纳、抽象出数列的规律的能力,分析题意,找到规律,并进行推导得出答案是解答此题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:填空题
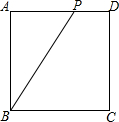 如图所示,正方形ABCD的边长为4cm,点P是AD边上的一个动点,则△ABP的面积S(cm2)与AP的长x(cm)之间的函数表达式为S=2x,x的取值范围是0<x<4.
如图所示,正方形ABCD的边长为4cm,点P是AD边上的一个动点,则△ABP的面积S(cm2)与AP的长x(cm)之间的函数表达式为S=2x,x的取值范围是0<x<4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
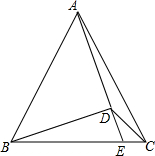 在△ABC中,AB=AC,以AB为斜边构成等腰Rt△ABD,∠ADB=90°,延长AD交BC于E,连接CD,∠DCB=45°.若S△ABE=15,CE=1,则AB=3$\sqrt{5}$.
在△ABC中,AB=AC,以AB为斜边构成等腰Rt△ABD,∠ADB=90°,延长AD交BC于E,连接CD,∠DCB=45°.若S△ABE=15,CE=1,则AB=3$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com