
分析 (1)求出方程x2-2x-8=0,根据新定义得出其“友好方程”的两根的两种情况,由根写出方程即可;
(2)解方程x2+cx+c-1=0可得x1=c-1,x2=-1,由新定义知两方程有公共根,据此可分①x=-1是两方程的公共根、②x=1-c是方程的公共根,两种情况分别求解可得;
(3)由“友好方程”定义结合(1)中的实例即可得.
解答 解:(1)解方程x2-2x-8=0得:x=-2或x=4,
则其“友好方程”的两根为:-2、-4或2、4,
若“友好方程”的两根为-2、-4,则该方程为(x+2)(x+4)=0,即x2+6x+8=0,
若“友好方程”的两根为2、4,则该方程为(x-2)(x-4)=0,即x2-6x+8=0;
(2)由方程x2+cx+c-1=0得:x1=c-1,x2=-1,
①若x=-1是两方程的公共根,代入方程x2+(b-1)x+b=0得:
(-1)2+(b-1)(-1)+b≠0,
则x=-1不是两方程公共解;
②若x=1-c是方程的公共根,则x=1是方程x2+(b-1)x+b=0的根,
代入,得:1+b-1+b=0,
解得:b=0,
则方程可化为x2-x=0,解得:x1=1,x2=0,
∴1-c=0,
∴c=1;
(3)①一个方程与其“友好方程”的常数项互为相反数;
②一个方程有两个“友好方程”,这两个“友好方程”的常数项相等,一次项互为相反数.
点评 本题主要考查一元二次方程的解法、解的概念,熟练掌握“友好方程”的定义是解题的关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:填空题
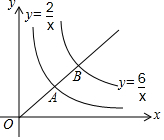 在同一坐标系中,反比例函数y=$\frac{2}{x}$和y=$\frac{6}{x}$分别与一个正比例函数在第一象限相交于A、B两点,则OA:OB=$\sqrt{3}$:3.
在同一坐标系中,反比例函数y=$\frac{2}{x}$和y=$\frac{6}{x}$分别与一个正比例函数在第一象限相交于A、B两点,则OA:OB=$\sqrt{3}$:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第n个 | |||||
| -3 | 9 | a | 81 | … | O |
| 1 | -3 | 9 | b | … | P |
| -2 | 10 | c | 82 | … | Q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com