
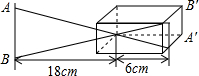
 如图,在针孔成像问题中,根据图形尺寸可知像A′B′的长是物AB长的( )
如图,在针孔成像问题中,根据图形尺寸可知像A′B′的长是物AB长的( )科目:初中数学 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
阅读下面的短文,并解答下列问题.
相似形开阔了人类的视野数学知识最初都产生于实践的需要,古人在测量土地面积和建筑物的高度时,就用到了相似形的知识.比如,几何学之父,古希腊人欧几里得曾经这样间接地测量金字塔的高度:他等到自己在阳光下的身影长与他的身高正好相等的时刻,测量了金字塔的塔影的长度.“这个,各位先生!”他宣布,“恰恰就是大金字塔的高度.”
如图(1),设A![]() 为塔高,B
为塔高,B![]() 为身高,由B
为身高,由B![]() ∥A
∥A![]() 知
知![]() ,当身影长与身高相等时,
,当身影长与身高相等时,![]() P=B
P=B![]() ,所以A
,所以A![]() =
=![]() P,即塔高等于塔影的长度.
P,即塔高等于塔影的长度.
光学望远镜、照相机的成像原理都用到相似形的知识,以简单的针孔成像为例,在方盒一侧壁开有极细的针孔,蜡烛发出的光线穿过针孔在方盒另一侧壁上形成一个倒立的像.蜡烛距方盒越远,所成像越小,像长和蜡烛长之间的比可以表示为![]() .如图(2)
.如图(2)

人眼观察远处的物体显得较小,其中的道理类似于以上针孔成像原理,只是人的眼球相当于照相机的光学镜头,成像原理稍复杂.
无数事实说明,相似形的知识使人类大大拓宽了视野,扩展了人类观察和认识事物的能力.
请你再举例说明相似形在实际生活、科学领域等方面的应用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com