
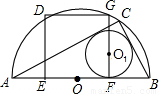
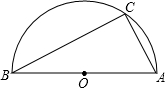
 EF,在Rt△ODE中利用勾股定理列式求解可得a=
EF,在Rt△ODE中利用勾股定理列式求解可得a=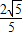 R,设BC、AC与⊙O1的切点分别为M、N,可得四边形O1MCN是正方形,根据正方形的性质可得MC=NC=r,设AF=x,BF=y,表示出AB、BC、AC,然后利用勾股定理列式整理得到x、y的关系,连接AG、BG可得△AGF和△GBF相似,利用相似三角形对应边成比例可得
R,设BC、AC与⊙O1的切点分别为M、N,可得四边形O1MCN是正方形,根据正方形的性质可得MC=NC=r,设AF=x,BF=y,表示出AB、BC、AC,然后利用勾股定理列式整理得到x、y的关系,连接AG、BG可得△AGF和△GBF相似,利用相似三角形对应边成比例可得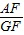 =
=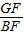 ,求出a2=xy,然后整理得到R、r的方程,解方程用R表示出r,然后求出比例即可;
,求出a2=xy,然后整理得到R、r的方程,解方程用R表示出r,然后求出比例即可;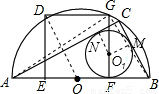 解:(1)连接OD,
解:(1)连接OD, EF=
EF= a,
a, a)2,
a)2, R2,
R2, R,
R,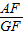 =
=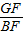 ,
,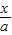 =
=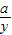 ,
, R2=2Rr+r2,
R2=2Rr+r2,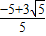 R,r2=
R,r2=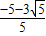 R(舍去),
R(舍去),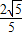 R:R:
R:R: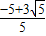 R=2
R=2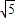 :5:(-5+3
:5:(-5+3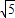 );
);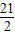 .
.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
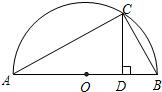 为D,AD=a,DB=b.
为D,AD=a,DB=b.| ab |
查看答案和解析>>
科目:初中数学 来源: 题型:
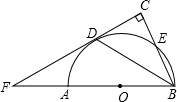 C,直线CD交BA的延长线于点F.
C,直线CD交BA的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有
如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com