Question

19．如图①，OA=2，OB=4，以A点为顶点、AB为腰在第三象限作等腰直角△ABC．
（1）点C的坐标为（-6，-2）；
（2）如图②，P是y轴负半轴上一个动点，当P点向y轴负半轴向下运动时，若以P为直角顶点，PA为腰作等腰直角△APD，过点D作DE⊥x轴于点E，则OP-DE的值为2；
（3）如图③，已知点F坐标为（-4，-4），当G在y轴运动时，作等腰直角△FGH，并始终保持∠GFH=90°，FG与y轴交于点G（0，m），FH与x轴交于点H（n，0），则m与n的关系为m+n=-8．

Answer 1

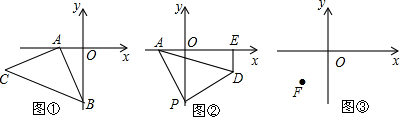
分析 （1）要求点C的坐标，则求C的横坐标与纵坐标，因为AC=AB，则作CM⊥x轴，即求CM和AM的值，容易得△MAC≌△OBA，根据已知即可求得C点的值；
（2）求OP-DE的值，则将其放在同一直线上，过D作DQ⊥OP于Q点，即是求PQ的值，由图易求得△AOP≌△PDQ（AAS），即可求得PQ的长；
（3）根据（2）的结论，可知m+n为定长，过F分别作x轴和y轴的垂线，运用（2）中的方法即可求得m+n的值．

解答 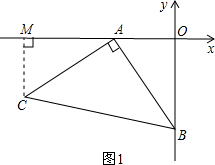解：（1）如图1，过C作CM⊥x轴于M点，
∵CM⊥OA，AC⊥AB，
∴∠MAC+∠OAB=90°，∠OAB+∠OBA=90°，
∴∠MAC=∠OBA，
在△MAC和△OBA中，
$\left\{\begin{array}{l}{∠CMA=∠AOB=90°}\\{∠MAC=∠OBA}\\{AC=BA}\end{array}\right.$，
∴△MAC≌△OBA（AAS），
∴CM=OA=2，MA=OB=4，
∴OM=6，
∴点C的坐标为（-6，-2），
故答案为（-6，-2）；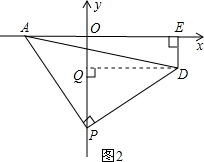

（2）如图2，过D作DQ⊥OP于Q点，则四边形OEDQ是矩形，
∴DE=OQ，
∵∠APO+∠QPD=90°，∠APO+∠OAP=90°，
∴∠QPD=∠OAP，
在△AOP和△PDQ中
$\left\{\begin{array}{l}{∠AOP=∠PQD=90°}\\{∠QPD=∠OAP}\\{AP=PD}\end{array}\right.$，
∴△AOP≌△PDQ（AAS），
∴AO=PQ=2，
∴OP-DE=OP-OQ=PQ=OA=2，
故答案为：2；

（3）m+n=-8．
理由：如图3，过点F分别作FS⊥x轴于S点，FT⊥y轴于T点，则∠HSF=∠GTF=90°=∠SOT，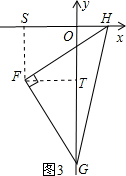
∴四边形OSFT是正方形，
∴FS=FT=4，∠EFT=90°=∠HFG，
∴∠HFS=∠GFT，
在△FSH和△FTG中，
$\left\{\begin{array}{l}{∠HSF=∠GTF}\\{∠HFS=∠GFT}\\{HF=GF}\end{array}\right.$，
∴△FSH≌△FTG（AAS），
∴GT=HS，
又∵G（0，m），H（n，0），点F坐标为（-4，-4），
∴OT═OS=4，
∴GT=-4-m，HS=n-（-4）=n+4，
∴-4-m=n+4，
∴m+n=-8．
当点H在点S的左侧，点G在点T的上方时，
同理可得△FSH≌△FTG，
∴GT=HS，
又∵G（0，m），H（n，0），点F坐标为（-4，-4），
∴OT═OS=4，
∴GT=m-（-4）=m+4，HS=n-（-4）=-4-n，
∴-4-n=m+4，
∴m与n的关系为m+n=-8．
故答案为：m+n=-8．

点评 本题属于三角形综合题，主要考查了三角形全等的判定和性质，矩形、正方形的性质的综合应用．解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等进行计算求解，解题时注意数形结合思想的运用．