
����Ŀ����ͼ����֪������![]() ��
��![]() ��������
��������![]() ����
����![]() ������������ν���A,B���㣬��
������������ν���A,B���㣬��![]() �ύ�ڵ�C��������B��ֱ��
�ύ�ڵ�C��������B��ֱ��![]() �������ߵ���һ����ΪD.
�������ߵ���һ����ΪD.
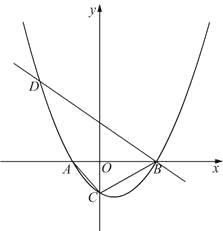
��1������D�ĺ�����Ϊ-5���������ߵĺ�������ʽ��
��2�����ڵ�һ�������������е�P��ʹ����A��B��PΪ���������������ABC���ƣ���![]() ��ֵ��
��ֵ��
��3���ڣ�1���������£���FΪ�߶�BD��һ�㣨�����˵㣩������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ. ����F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3��F
����3��F![]() .
.
��������
���⣨1�����ݵ��������ϵ���������㷽�̵Ĺ�ϵ���������![]() ��ֵ�õ�ֱ�ߵĽ���ʽ����D�������ꡢ
��ֵ�õ�ֱ�ߵĽ���ʽ����D�������ꡢ![]() ��ֵ�õ������ߵĺ�������ʽ.
��ֵ�õ������ߵĺ�������ʽ.
��BM=9��AB=6����BF=![]() ��BD=
��BD=![]() ��AF=
��AF=![]()
��2������PAB�ס�ABC����PAB�ס�BAC����������ۼ���.
��3������D��DH��y���ڵ�H������A��AG��DH�ڵ�G����BD�ڵ�F�����F��Ϊ���������ǣ����ڵ�M���߶�AF����ÿ��1����λ���ٶ��˶������߶�FD����ÿ��2����λ���ٶ��˶����Ӷ�����ֱ��BD����б����30��֪��![]() ���ָ��ݴ�ֱ�߶���̵�����֪��F��Ϊ���Ӷ����ݺ�30��ֱ�������ε�������⼴��.
���ָ��ݴ�ֱ�߶���̵�����֪��F��Ϊ���Ӷ����ݺ�30��ֱ�������ε�������⼴��.
�����������1����������![]() ��
��![]() ��������
��������![]() ����
����![]() ������������ν���A,B���㣬
������������ν���A,B���㣬
��A��-2��0����B��4��0��.
����B��ֱ��![]() �ϣ���
�ϣ���![]() ����
����![]() .
.
��ֱ�ߵĽ���ʽΪ![]() .
.
����D��ֱ��![]() �ϣ��Һ�����Ϊ-5����������Ϊ
�ϣ��Һ�����Ϊ-5����������Ϊ![]() .
.
����D��������![]() �ϣ���
�ϣ���![]() �����
�����![]() .
.
�������ߵĺ�������ʽΪ![]() .
.
��2���ã���C������Ϊ![]() ����
����![]() .
.
���P������Ϊ![]() ��
��
�����������
������PAB�ס�ABC������PAB=��ABC��![]() .
.
������PAB=��ABC ��![]() ����
����![]() .
.
��![]() �����
�����![]() .
.
��ʱ��P������Ϊ![]() ��
��![]() ��
��
����![]() ��
��![]() �����
�����![]() .
.
������PAB�ס�BAC������PAB=��BAC��![]() .
.
������PAB=��BAC ��![]() ����
����![]() .
.
��![]() �����
�����![]() .
.
��ʱ��P������Ϊ![]() ��
��![]() ��
��
����![]() ��
��![]() �����
�����![]() .
.

��3����ͼ������D��DH��y���ڵ�H������A��AG��DH�ڵ�G����BD�ڵ�F�����F��Ϊ����.
��ֱ��BD�Ľ���ʽΪ![]() �����FBA=��FGD=30��.
�����FBA=��FGD=30��.
��AB=6����AF=![]() .
.
����F������Ϊ![]() .
.



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ������ֱ���
������ֱ���![]() ������
������![]() ����
����![]() ������
������![]() ����ƽ�ƣ�ʹ��O�ƶ�����M���õ�
����ƽ�ƣ�ʹ��O�ƶ�����M���õ�![]() ����
����![]() �ֱ��Ӧ��
�ֱ��Ӧ��![]() ��.
��.
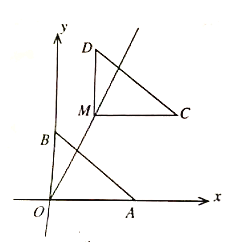
��1����գ�m��ֵΪ_____________����C��������______________��
��2��������![]() ���Ƿ����һ��N��ʹ
���Ƿ����һ��N��ʹ![]() ��������ڣ��������N�����ꣻ��������ڣ���˵�����ɣ�
��������ڣ��������N�����ꣻ��������ڣ���˵�����ɣ�
��3������![]() ����P������
����P������![]() ��һ���㣬��ֱ��д��ʹ
��һ���㣬��ֱ��д��ʹ![]() �ǵ���������ʱ��P������.
�ǵ���������ʱ��P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������¥�IJ��ֽ��漰���������ͼ��С���ڼ�¥A��������E������¥F�����ֻ��֣���ʱA,E,F��ͬһֱ����.�ܵ�һ¥ʱ������Ա���ڽ�����ˮ���ˮ��·�߳������ߣ���1.2m�ߵ�D�������ˮ�����þ���E,F. ����B�͵�E����C��F����ظ߶ȷֱ���ͬ��������Ա��ˮ������������ƽ��0.4m�������������____m��ǡ�ð�ˮ�絽F���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��չ��չ�γ�չʾ�����Ҫ����A��B�����ͺŵ�������湲20������֪A��B���ֹ���Ƶĵ��۷ֱ�Ϊ40Ԫ��70Ԫ
��1�������ݻ��Ҫ��A�ֹ����������B�ֹ��������֮��Ϊ3��2����Ҫ���ٷ��ã�
��2����������A��B�����ͺŵ���������ƣ�����B���ͺŲ�����5���������ܷ��ò�����1000Ԫ�����м�������������ÿһ�����������ķ��÷ֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
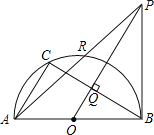
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����C�ǰ�ԲO��һ�㣬![]() �ڵ�Q������B����ԲO�����ߣ���OQ���ӳ����ڵ�P��PA����ԲO��R�������е�ʽ����ȷ���ǣ� ��
�ڵ�Q������B����ԲO�����ߣ���OQ���ӳ����ڵ�P��PA����ԲO��R�������е�ʽ����ȷ���ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����EΪ����ABCD�ı�AD��һ�㣬��P�ӵ�B������BE��ED��DC�˶�����Cֹͣ����Q�ӵ�B������BC�˶�����Cֹͣ�������˶����ٶȶ���1cm/s������P��Qͬʱ��ʼ�˶������˶�ʱ��Ϊt��s������BPQ�����Ϊy��cm2������֪y��t֮��ĺ���ͼ����ͼ2��ʾ���������н��ۣ�����0��t��10ʱ����BPQ�ǵ��������Σ���S��ABE=48cm2����14��t��22ʱ��y=110��5t�������˶������У�ʹ����ABP�ǵ��������ε�P��һ����3����������BPQ����BEA����ʱ��t=14.5��������ȷ���۵�����ǣ�������

A. �٢ܢ� B. �٢ڢ� C. �٢ۢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
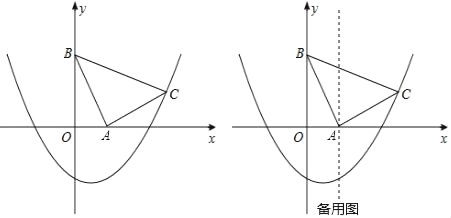
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ABC�ǵ���ֱ�������Σ���BAC��90�㣬A(1��0)��B(0��2)�����κ���y��![]() x2+bx��2��ͼ��C�㣮
x2+bx��2��ͼ��C�㣮
(1)����κ����Ľ���ʽ��
(2)ƽ�Ƹö��κ���ͼ��ĶԳ�������ֱ��l����ֱ��lǡ�ý���ABC�������Ϊ1��2�����֣��������ʱֱ��l��x��Ľ������ꣻ
(3)����ABC��AC����ֱ��Ϊ�Գ��ᷭ��180�㣬�õ���AB��C����ô�ڶ��κ���ͼ�����Ƿ���ڵ�P��ʹ��PB��C����B��CΪֱ�DZߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������|a��1|+|a��2|+|a��3|+��+|a��2019|��Сֵ�Ƕ��٣�
���Ķ����⣩
Ϊ�˽��������⣬�����ȴ����������֣�|a|�ļ���������a������������϶�Ӧ�ĵ㵽ԭ��ľ��룮��ô|a��1|���Կ���a������������϶�Ӧ�ĵ㵽1�ľ��룻|a��1|+|a��2|�Ϳ��Կ���a������������϶�Ӧ�ĵ㵽1��2������ľ���֮�ͣ��������ǽ�������о�|a��1|+|a��2|����Сֵ��
�����ȿ�a��ʾ�ĵ���ܵ�3���������ͼ��ʾ��
��1����ͼ����a��1����ߣ���ͼ�к����Կ��Կ���a��1��2�ľ���֮�ʹ���1��
��2����ͼ����a��1��2֮�䣨������1��2�ϣ������Կ���a��1��2�ľ���֮�͵���1��
��3����ͼ����a��2���ұߣ���ͼ�к����Կ��Կ���a��1��2�ľ���֮�ʹ���1��
����������
��1��|a��2|+|a��5|�ļ����������� ��������������̽����|a��2|+|a��5|����Сֵ���� ����
��2��|a��1|+|a��2|+|a��3|�ļ����������� ��������������̽����|a��1|+|a��2|+|a��3|����Сֵ���� ��������ͼ��������������õ���Сֵʱa���ڵ�λ�ã��ɴ˿��Եó�aΪ�� ����
��3�����|a��1|+|a��2|+|a��3|+|a��4|+|a��5|����Сֵ��
��4�����|a��1|+|a��2|+|a��3|+��+|a��2019|����Сֵ��
����չӦ�ã�
����ͼ���������ϱ�ʾ��a��ʹ����2��5�ľ���֮��С��4����ֱ��д��a�ķ�Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Բ��һ����Բ���������ij߹���ͼ����.
��֪����O�͡�O��һ��P��
��������O������MN��ʹMN������P��

��������ͼ��
��1��������OP��
��2���Ե�PΪԲ�ģ�С��OP�ij�Ϊ�뾶����������OP��A��B���㣻
��3���ֱ��Ե�A��BΪԲ�ģ��Դ���![]() ��Ϊ�뾶��������������M��N���㣻
��Ϊ�뾶��������������M��N���㣻
��4����ֱ��MN.��MN�����������ġ�O�����ߣ�
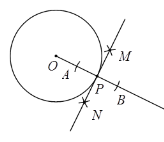
��ش𣺸ó߹���ͼ��������____________________________________________________________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com