
【题目】随着“一带一路”的进一歩推进,我国瓷器(“china”)更为“一带一路”沿践人民所推崇,一外国商户准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比每个茶杯多120元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)4套茶具的批发价为1280元.
根据以上僖息:
(1)求每个茶壶与每个茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多18个,并且茶壶和茶杯的总数不超过320个,该商户计划将一半的茶具按每套500元成套销售,其余按每个茶壶300元,每个茶杯80元零售.没核商户购进茶壶m个.
①试用含m的关系式表示出该商户计划获取的利润;
②请帮助他设计一种获取利润最大的方案,并求出最大利润.
【答案】(1)茶杯的批发价为40元/个,则茶壶的批发价为160元/个;
(2)①w=280m+720;
②当购进50个茶壶、268个茶杯时,有最大利润,最大利润为14720元.
【解析】
(1)设茶杯的批发价为x元/个,则茶壶的批发价为(x+120)元/个,根据总价=单价×数量即可得出关于x的一元一次方程,解之即可得出结论;
(2)①设商户购进茶壶m个,则购进茶杯(5m+18)个,设利润为w,根据总利润=单件利润×销售数量结合销售方式,即可得出w关于m的函数关系式;
②利用一次函数的性质即可解决最值问题.
(1)设茶杯的批发价为x元/个,则茶壶的批发价为(x+120)元/个,
根据题意得:4(4x+x+120)=1280,
解得:x=40,
∴x+120=160.
答:茶杯的批发价为40元/个,则茶壶的批发价为160元/个;
(2)①设商户购进茶壶m个,则购进茶杯(5m+18)个,
若利润为w元,则w=![]() (5001604×40)+
(5001604×40)+![]() (300-160)+(5m+182m)×(8040)=280m+720;
(300-160)+(5m+182m)×(8040)=280m+720;
②由题意得m+5m+18≤320,
得m≤![]() ,
,
∵w随着m的增大而增大,
∴当m取最大值时,利润w最大,
∵m≤![]() ,
,
∴当m=![]() 时,w=14720.
时,w=14720.
∴当购进50个茶壶、268个茶杯时,有最大利润,最大利润为14720元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若
,若![]() ,
,![]() 满足
满足![]() ,则点
,则点![]() 就称为“绝好点”.例如:
就称为“绝好点”.例如:![]() ,因为
,因为![]() ,所以
,所以![]() 是“绝好点”.
是“绝好点”.
(1)点![]() “绝好点”;点
“绝好点”;点![]() “绝好点”(填“是”或“不是);
“绝好点”(填“是”或“不是);
(2)已知一次函数![]() (
(![]() 为常数)图像上有一个“绝好点”的坐标是
为常数)图像上有一个“绝好点”的坐标是![]() ,一次函数
,一次函数![]() (
(![]() 为常数)图像上是否存在其他“绝好点”?若存在,请求出来;若不存在,请说明理由;
为常数)图像上是否存在其他“绝好点”?若存在,请求出来;若不存在,请说明理由;
(3)点![]() 和点
和点![]() 为一次函数
为一次函数![]() (
(![]() 为常数且
为常数且![]() )图像上的两个“绝好点”,点
)图像上的两个“绝好点”,点![]() 在
在![]() 轴上运动,当
轴上运动,当![]() 最小时,求点
最小时,求点![]() 的坐标.(用含字母
的坐标.(用含字母![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图像,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
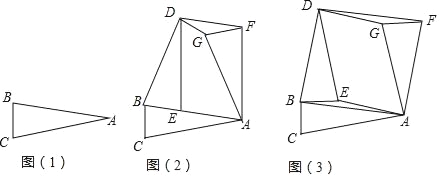
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
(1)创新小组将图(1)中的△ABC以点B为旋转中心,逆时针旋转角度α,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转角度α,得到△AFG,连接DF,得到图(2),则四边形AFDE的形状是 .
(2)实践小组将图(1)中的△ABC以点B为旋转中心,逆时针逆转90°,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°,得到△AFG,连接DF、DG、AE,得到图(3),发现四边形AFDB为正方形,请你证明这个结论.
拓展探索
(3)请你在实践小组操作的基础上,再写出图(3)中的一个特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
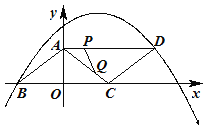
【题目】如图,□ABCD的两个顶点B,D都在抛物线y=![]() x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB=![]() .
.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点E,使以A,C,D,E为顶点的四边形是菱形?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)动点P从点A出发向点D运动,同时动点Q从点C出发向点A运动,运动速度都是每秒1个单位长度,当一个点到达终点时另一个点也停止运动,运动时间为t(秒).当t为何值时,△APQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空,如图,已知∠A=∠F,∠C=∠D,试说明 BD∥CE.

解:∵∠A=∠F(已知),
∴ ∥ ( ),
∴∠D+∠DBC=180°( ),
又∵∠C=∠D(已知),
∴∠C+∠DBC=180°(等量代换),
∴BD∥CE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程![]() 与行驶的时间
与行驶的时间![]() 之间的函数关系,如图中线段AB所示.慢车离乙地的路程
之间的函数关系,如图中线段AB所示.慢车离乙地的路程![]() 与行驶的时间
与行驶的时间![]() 之间的函数关系,如图中线段OC所示.根据图象进行以下研究.
之间的函数关系,如图中线段OC所示.根据图象进行以下研究.
![]() 快车的速度是________
快车的速度是________![]() ,慢车的速度是________
,慢车的速度是________![]() ;
;
![]() 求AB与OC的函数关系式.
求AB与OC的函数关系式.
![]() 何时快车离乙地的距离大于慢车离乙地的距离?
何时快车离乙地的距离大于慢车离乙地的距离?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com