
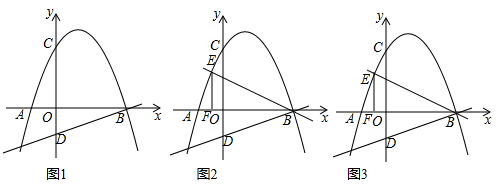
分析 (1)由点的直线上,点的坐标符合函数解析式,代入即可;
(2)先求出OB,OD再利用锐角三角函数求出BF=2EF,由它建立方程4-t=2×[-$\frac{1}{2}$(t+m)(t-4)],求解即可;
(3)先判断出△PEQ≌△DBO,表示出点P(t+4,-$\frac{1}{2}$(t+m)(t-4))+2),再利用它在抛物线 y=-$\frac{1}{2}$(t+m)(t-4)上求解.
解答 解:(1)∵抛物线y=-$\frac{1}{2}$(x+m)(x-4)(m>0)交x轴于点A、B(A左B右)
当y=0时,0=-$\frac{1}{2}$(x+m)(x-4),
∴x1=-m,x2=4
∴A(-m,0),B(4,0)
∵点B在直线y=$\frac{1}{2}$x+b上,
∴4×$\frac{1}{2}$+b=0,b=-2
∴直线y=$\frac{1}{2}$x-2,
当x=0时y=-2
∴D(0,-2),
(2)设E(t,-$\frac{1}{2}$(t+m)(t-4)),
∵EF⊥x轴,
∴∠EFO=90° EF∥y轴,
∴F(t,0),
由(1)可知D(0,-2)B(4,0),
∴OD=2 OB=4,
∴在Rt△BDO中,tan∠DBO=$\frac{OD}{OB}$=$\frac{1}{2}$,
∵直线BD沿x轴翻折得到BE,
∴∠DBO=∠EBF,
∴tan∠DBO=tan∠EBF,
∴tan∠EBF=$\frac{1}{2}$,
∴$\frac{EF}{BF}$=$\frac{1}{2}$,
∴BF=2EF,
∴EF=-$\frac{1}{2}$(t+m)(t-4)BF=4-t
∴4-t=2×[-$\frac{1}{2}$(t+m)(t-4)]
∴t+m=1,
∴AF=t-(-m)=t+m=1,
∴AF=1,
(3)如图,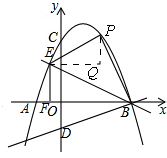
过点E作x轴的平行线,过点P作y轴的平行线交于点Q
设EP交y轴于点M
∵四边形BDEP是平行四边形
∴EP∥DB EP=DB
∵EP∥DB PQ∥y轴,
∴∠EMD=∠ODB∠EMD=∠EPQ,
∴∠ODB=∠EPQ,
∵∠PQE=∠DOB=90° EP=BD,
∴△PEQ≌△DBO,
∴PQ=OD=2 EQ=OB=4,
∵E(t,-$\frac{1}{2}$(t+m)(t-4)),
∴P(t+4,-$\frac{1}{2}$(t+m)(t-4)+2),
∵P(t+4,-$\frac{1}{2}$(t+m)(t-4))+2)在抛物线 y=-$\frac{1}{2}$(t+m)(t-4)上
∴-$\frac{1}{2}$(t+4+m)(t+4-4)=-$\frac{1}{2}$(t+m)(t-4)+2
∵t+m=1,
∴t=-2,
∵t+m=1,
∴m=3,
∴-$\frac{1}{2}$(t+m)(t-4)+2=5,
∴P(2,5)
点评 此题是二次函数综合题,主要考查图象上的点的特点,三角形的全等的性质和判定,翻折的性质,解本题的关键是表示出点的坐标.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
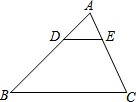 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )| A. | $\frac{AE}{EC}$=$\frac{1}{3}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ②④ | B. | ①③ | C. | ②③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.28×1013 | B. | 4.28×1012 | C. | 4.28×1011 | D. | 4.28×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2a-1 | D. | -4027 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com