
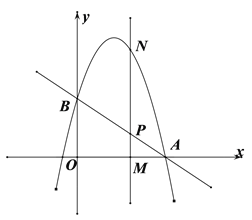
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 当
当![]() 时,求m的值.
时,求m的值.
【答案】⑴![]() ,
, ![]() ⑵
⑵![]() ⑶有两解,N点在AB的上方或下方, m=
⑶有两解,N点在AB的上方或下方, m=![]() 与m=
与m=![]()
【解析】整体分析:
(1)把A(3,0)代入y=kx+2中求k值,把x=0代入y=kx+2,求出B点的坐标,由A,B的坐标求二次函数的解析式;(2)①用含m的式子表示出NP的长,由平行四边形的性质得OB=PN列方程求解;②连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H, 设GH=BH=t,由![]() ,用t表示AH,AG,由AB=
,用t表示AH,AG,由AB=![]() ,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
,求t的值,求直线BG,BN的解析式,分别与抛物线方程联立求解.
解:⑴![]() ,
,
二次函数的表达式为![]()
⑵如图,设M(m,0),
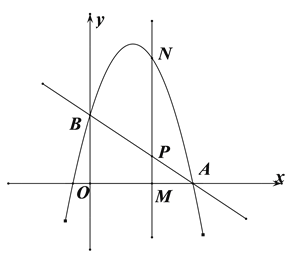
则p(m, ![]() ),N(m,
),N(m, ![]()
![]() =
=![]()
=![]()
由于四边形OBNP为平行四边形得PN=OB=2,
解方程![]() .
.
即![]()
⑶有两解,N点在AB的上方或下方,m=![]() 与m=
与m=![]() .
.
如图连接BN,过点B作BN的垂线交x轴于点G,过点G作BA的垂线,垂足为点H.
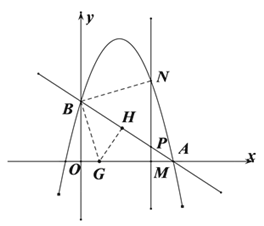
由![]() 得
得![]() ,
,
从而设GH=BH=t,则由![]() ,得AH=
,得AH= ![]() ,
,
由AB=t+ ![]() =
=![]() ,解得t=
,解得t=![]() ,
,
从而OG=OA-AG=3-![]() =
=![]() .即G(
.即G(![]() )
)
由B(0,2),G(![]() )得
)得![]() .
.
将![]() 分别与
分别与![]() 联立,
联立,
解方程组得m=![]() ,m=
,m=![]() .
.
故m=![]() 与m=
与m=![]() .
.


科目:初中数学 来源: 题型:
【题目】(8分)如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.(1)求证: AE=AF; (2)若AG=4,AC=7,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (
(![]() ,
, ![]() )的图象与直线
)的图象与直线![]() 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
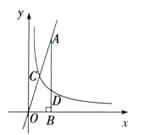
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确实一点M,使点M到C、D两点距离之和d=MC+MD,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=_____;若S△ABC=12,则S△ADF﹣S△BEF=_____.
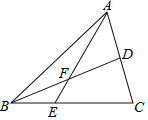
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.
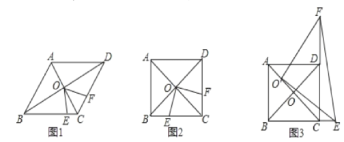
(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系___;
(2)如图1,当∠ABC=90°时,若AC=4![]() ,BE=
,BE=![]() ,求线段EF的长;
,求线段EF的长;
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按如图所示的程序计算,如果开始输入的x的值为48,我们发现第一次输出得到的结果为24,第二次输出的结果为12,第三次得到的输出结果为6,……,则第2019次得到的结果为__.
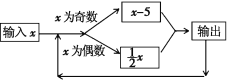
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理
表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理![]() 也可理解为
也可理解为![]() 与3两数在数轴上所对应的两点之间的距离,
与3两数在数轴上所对应的两点之间的距离,![]() 就表示
就表示![]() 在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求![]() .
.
(2)若![]() ,则
,则![]() .
.
(3)请你找出所有符合条件的整数![]() ,使得
,使得![]() .
.
(4)求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 的取值情况.
的取值情况.
(5)已知![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某项工程如果由乙单独完成比甲单独完成多用6天;如果甲、乙先合做4天后,再由乙单独完成,那么乙一共所用的天数刚好和甲单独完成工程所用的天数相等.
(1)求甲单独完成全部工程所用的时间;
(2)该工程规定须在20天内完成,若甲队每天的工程费用是4.5万元,乙队每天的工程费用是2.5万元,请你选择上述一种施工方案,既能按时完工,又能使工程费用最少,并说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com