

 ,
,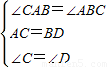 ,
,

 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:新课标教材导学 数学九年级(第一学期) 题型:044
如图,已知BC与AD交于点O,BC=AD,如果要得到△ACB≌△BDA还需要补充一个什么条件?至少写出3个不同的答案,并写出每种答案中证明全等的依据.
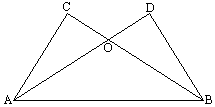
查看答案和解析>>
科目:初中数学 来源:2012-2013学年湖北省武汉市元月调考九年级(上)数学热身卷(五)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com