
【题目】如图,在Rt△ABC中,AC=BC,点D是△ABC内一点,若AC=AD,∠CAD=30°,连接BD,则∠ADB的度数为( )
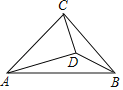
A.120°B.135°C.150°D.165°
【答案】B
【解析】
先根据△ABC是等腰直角三角形得:∠CAB=∠ABC=45°,作辅助线,构建全等三角形,证明△CDB≌△AED,则∠ADE=∠CBD,ED=BD,设∠CBD=x,则∠ADE=x,∠DEB=∠DBE=15+x,根据∠ABC=45°列方程可求x的值,根据三角形内角和得∠BDC=150°,最后由周角得出结论.
∵AC=BC,∠ACB=90°,
∴∠CAB=∠ABC=45°,
∵AC=AD,
∴AD=BC,
∵∠CAD=30°,
∴∠ACD=∠ADC=75°,
∠DAB=45°﹣30°=15°,
∴∠DCB=90°﹣75°=15°,
∴∠EAD=∠DCB,
在AB上取一点E,使AE=CD,连接DE,
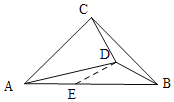
在△CDB和△AED中,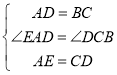 ,
,
∴△CDB≌△AED(SAS),
∴∠ADE=∠CBD,ED=BD,
∴∠DEB=∠DBE,
设∠CBD=x,则∠ADE=x,∠DEB=∠DBE=15+x,
∵∠ABC=45°,
∴x+15+x=45,
∴x=15°,
∴∠DCB=∠DBC=15°,
∴∠BDC=180°﹣15°﹣15°=150°,
∴∠ADB=360°﹣75°﹣150°=135°;
故选:B.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
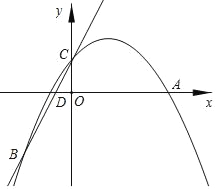
【题目】已知抛物线y=ax2+bx+2过点A(5,0)和点B(﹣3,﹣4),与y轴交于点C.
(1)求抛物线y=ax2+bx+2的函数表达式;
(2)求直线BC的函数表达式;
(3)点E是点B关于y轴的对称点,连接AE、BE,点P是折线EB﹣BC上的一个动点,
①当点P在线段BC上时,连接EP,若EP⊥BC,请直接写出线段BP与线段AE的关系;
②过点P作x轴的垂线与过点C作的y轴的垂线交于点M,当点M不与点C重合时,点M关于直线PC的对称点为点M′,如果点M′恰好在坐标轴上,请直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
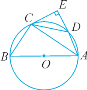
【题目】如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,连接CD且DC=BC,过C点作AD的垂线交AD延长线于E.
(1)求证:CE是⊙O的切线;
(2)若AB=5,AC=4,求tan∠DCE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).
(1)求y与x之间的函数表达式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
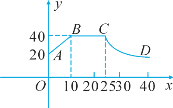
【题目】心理学家研究发现,一般情况下,在一节40分钟的课中,学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数解析式,并写出自变量的取值范围;
(2)开始上课后第5分钟时与第30分钟时比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数至少为36,那么经过适当安排,老师能否在学生达到所需的状态下讲解完这道题目?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
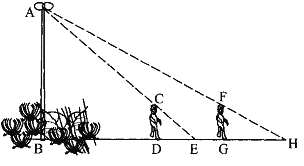
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是( )
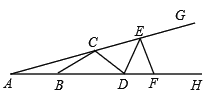
A. 80° B. 90° C. 100° D. 108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.

求证:(1)△DEF∽△BDE;(2)DGDF=DBEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程mx2﹣(2m﹣2)x+m=0有实根.
(1)求m的取值范围;
(2)若原方程两个实数根为x1,x2,是否存在实数m,使得![]() =1?请说明理由.
=1?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com