
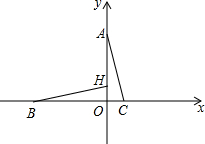
 如图扇形OAB的圆心角为120°,半径为6cm.
如图扇形OAB的圆心角为120°,半径为6cm.科目:初中数学 来源: 题型:
 |
| AB |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AB |
| 1 |
| 3 |
 |
| AB |
| 19 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
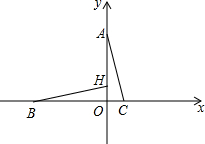
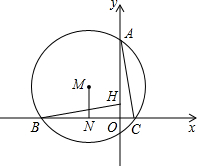
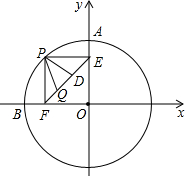
 上异于A,B的动点,PE⊥OA于点E,PF⊥OB于点F,D,Q在EF上,且ED=DQ=QF.①当点P在
上异于A,B的动点,PE⊥OA于点E,PF⊥OB于点F,D,Q在EF上,且ED=DQ=QF.①当点P在  上运动时,在线段PE,PD,ED中,是否存在长度不变的线段?若存在,请求出该线段的长度,若不存在,请说明理由.②PE2+3PQ2的值是定值吗?若是,请求出这个定值,若不是,请说明理由.
上运动时,在线段PE,PD,ED中,是否存在长度不变的线段?若存在,请求出该线段的长度,若不存在,请说明理由.②PE2+3PQ2的值是定值吗?若是,请求出这个定值,若不是,请说明理由.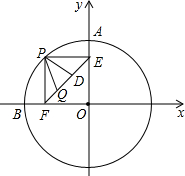
查看答案和解析>>
科目:初中数学 来源:2008-2009学年湖北省武汉市青山区九年级(上)期中数学试卷(解析版) 题型:解答题
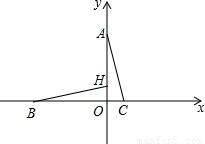
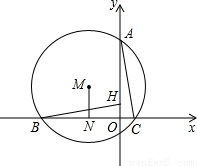
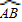 上异于A,B的动点,PE⊥OA于点E,PF⊥OB于点F,D,Q在EF上,且ED=DQ=QF.①当点P在
上异于A,B的动点,PE⊥OA于点E,PF⊥OB于点F,D,Q在EF上,且ED=DQ=QF.①当点P在 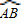 上运动时,在线段PE,PD,ED中,是否存在长度不变的线段?若存在,请求出该线段的长度,若不存在,请说明理由.②PE2+3PQ2的值是定值吗?若是,请求出这个定值,若不是,请说明理由.
上运动时,在线段PE,PD,ED中,是否存在长度不变的线段?若存在,请求出该线段的长度,若不存在,请说明理由.②PE2+3PQ2的值是定值吗?若是,请求出这个定值,若不是,请说明理由.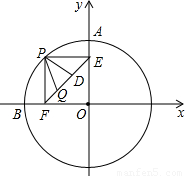
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com