【题目】化简求值：
(1)
，其中
；
(2)若
，且
，求
的值。
【答案】（1）
；（2）3
【解析】（1）先算乘法，再合并同类项，最后代入求出即可；
（2）根据（x+2）（y+2）=3即可求得xy的值，根据x+y=1两边同时平方即可求得x2+y2，代入即可求得所求的式子的值．
（1）（x+2）2+（2x+1）（2x-1）-4x（x+1）
=x2+4x+4+4x2-1-4x2-4x
=x2+3，
当x=-2时，原式=4+3=7．
（2）∵x+y=1，
∴x2+y2+2xy=1，
∴x2+y2=1-2xy，
∵（x+2）（y+2）=3，
∴xy+（x+y）+4=3，
∴xy+1+4=3，
∴xy=-2，
∴x2+xy+y2=1-2xy+xy=1-xy=1-（-2）=3．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】八(2)班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表(10分制)：
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分，乙队成绩的众数是 分；
(2)计算乙队的平均成绩和方差；
(3)已知甲队成绩的方差是1.4，则成绩较为整齐的是 队．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用四个长为m，宽为n的相同长方形按如图方式拼成一个正方形．
(1).请用两种不同的方法表示图中阴影部分的面积．
方法①： ；
方法②： ．
(2).由 (1)可得出
2，
，4mn这三个代数式之间的一个等量关系为： ．
(3)利用(2)中得到的公式解决问题：已知2a+b=6，ab＝4，试求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场购进一种每件价格为100元的新商品，在商场试销发现：销售单价x（元/件）与每天销售量y（件）之间满足如图所示的关系：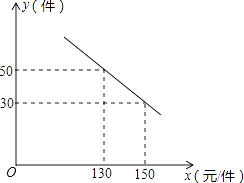 
（1）求出y与x之间的函数关系式；
（2）写出每天的利润W与销售单价x之间的函数关系式；若你是商场负责人，会将售价定为多少，来保证每天获得的利润最大，最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了鼓励居民节约用水，某市自来水公司对每户月用水量进行计费，每户每月用水量在规定吨数以下的收费标准相同；规定吨数以上的超过部分收费标准相同，以下是小明家
月份用水量和交费情况：
月份 |
|
|
|
|
|
用水量（吨） |
|
|
|
|
|
费用（元） |
|
|
|
|
|
根据表格中提供的信息，回答以下问题：
求出规定吨数和两种收费标准；
若小明家
月份用水
吨，则应缴多少元？
若小明家
月份缴水费
元，则月份用水多少吨？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，O为正方形对角线的交点，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连结DF，交BE的延长线于点G，连结OG．
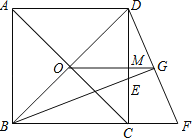
（1）求证：△BCE≌△DCF．
（2）判断OG与BF有什么关系，证明你的结论．
（3）若DF2=8-4
，求正方形ABCD的面积？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某厂仓库储存了部分原料，按原计划每时消耗2 t，可用60 h．由于技术革新，实际生产能力有所提高，即每时消耗的原料量大于计划消耗的原料量．设现在每时消耗原料x(单位：t)，库存的原料可使用的时间为y(单位：h)．
(1)写出y关于x的函数解析式，并求出自变量的取值范围；
(2)若恰好经过24 h才有新的原料进厂，为了使机器不停止运转，则x应控制在什么范围内？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
