
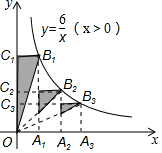
 如图,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{6}{x}$(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,图中阴影部分的面积之和为$\frac{49}{12}$.
如图,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{6}{x}$(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,图中阴影部分的面积之和为$\frac{49}{12}$. 分析 先根据反比例函数上的点向x轴、y轴引垂线形成的矩形面积等于|k|,得到S△OB1C1=S△OB2C2=S△OB3C3=$\frac{1}{2}$|k|=3,再根据相似三角形的面积比等于相似比的平方,得到3个阴影部分的三角形的面积,从而求得面积的和.
解答  解:由题可得${S}_{△O{B}_{1}{C}_{1}}={S}_{△O{B}_{2}{C}_{2}}={S}_{△O{B}_{3}{C}_{3}}=\frac{1}{2}k=3$,
解:由题可得${S}_{△O{B}_{1}{C}_{1}}={S}_{△O{B}_{2}{C}_{2}}={S}_{△O{B}_{3}{C}_{3}}=\frac{1}{2}k=3$,
∵OA1=A1A2=A2A3,且过点A1、A2、A3作y轴的平行线,
∴设图中阴影部分的面积从左往右依次为S1,S2,S3,则S1=3,
∵OA1=A1A2=A2A3,
∴S2:S△OB2C2=1:4,S3:S△OB3C3=1:9,
∴图中阴影部分的面积分别是3,$\frac{3}{4}$,$\frac{1}{3}$,
∴图中阴影部分的面积之和为:3+$\frac{3}{4}$+$\frac{1}{3}$=$\frac{49}{12}$.
故答案为:$\frac{49}{12}$.
点评 本题主要考查了反比例函数的性质,此题难度较大,综合性较强,注意反比例函数上的点向坐标轴作垂线形成的矩形面积等于反比例函数的k值的绝对值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
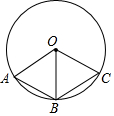 如图,OA,OB,OC是⊙O的三条半径.
如图,OA,OB,OC是⊙O的三条半径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com