
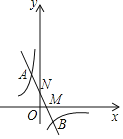
【题目】如图,关于x的一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A(﹣2,8),B(4,m)两点.
的图象相交于A(﹣2,8),B(4,m)两点.
(1)求一次函数与反比例函数的解析式.
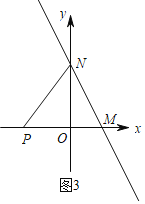
(2)设一次函数y=k1x+b的图象与x轴,y轴的交点分别为M,N,P是x轴上一动点,当以P,M,N三点为顶点的三角形是等腰三角形时,求点P的坐标.
【答案】(1)y=﹣![]() ,y=﹣2x+4;(2)点P的坐标是(﹣2,0)或(2+2
,y=﹣2x+4;(2)点P的坐标是(﹣2,0)或(2+2![]() ,0)或(2﹣2
,0)或(2﹣2![]() ,0)或(﹣3,0).
,0)或(﹣3,0).
【解析】
(1)先把A点坐标代入y=![]() 可求出k2的值,从而确定反比例函数解析式;再把B(4,m)代入反比例函数解析式求出m的值,可确定点B的坐标,然后利用待定系数法求一次函数解析式;
可求出k2的值,从而确定反比例函数解析式;再把B(4,m)代入反比例函数解析式求出m的值,可确定点B的坐标,然后利用待定系数法求一次函数解析式;
(2)先根据一次函数的解析式确定M和N的坐标,根据以P,M,N三点为顶点的三角形是等腰三角形分三种情况讨论:①NP=NM;②MP=MN;③PN=PM;前两种直接根据线段的长得出点P的坐标,第三种根据两点的距离列方程可得结论.
解:(1)把![]() ,
,![]() 代入反比例函数
代入反比例函数![]() 得:
得:![]() ,
,
![]() ,
,![]() ,
,
∴反比例函数解析式为![]() ,且
,且![]() ,
,
把![]() ,
,![]() 代入
代入![]() 得:
得: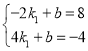 ,
,
解得![]() ,
,
∴一次函数解析式为![]() ;
;
(2)![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
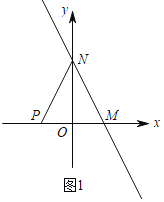
①当![]() 时,如图1,
时,如图1,
![]() ,
,
![]() ,
,
![]() ;
;
②当![]() 时,如图2,
时,如图2,
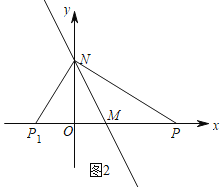
由勾股定理得:![]() ,
,
![]() ,
,![]() 或
或![]() ,
,![]() ;
;
③当![]() 时,如图3,
时,如图3,
![]() 是
是![]() 轴上一动点,
轴上一动点,
![]() 设
设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上,点![]() 的坐标是
的坐标是![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,点C在半圆上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC
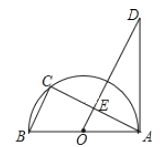
(1)求证:AD是半圆O的切线;
(2)求证:△ABC∽△DOA;
(3)若BC=2,CE=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
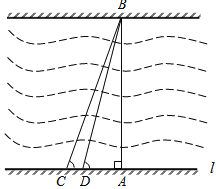
【题目】某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求:AB的长(精确到0.1米,参考数据:sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5).
查看答案和解析>>
科目:初中数学 来源: 题型:
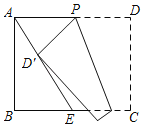
【题目】如图,在矩形ABCD中,AB=4,BC=6,E是BC的中点,连接AE,P是边AD上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点D′处,当△APD′是直角三角形时,PD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E是CD边上一点,![]() ,连接AE、BE、BD,且AE、BD交于点F.若
,连接AE、BE、BD,且AE、BD交于点F.若![]() ,则
,则![]() ( )
( )

A.15.5B.16.5C.17.5D.18.5
查看答案和解析>>
科目:初中数学 来源: 题型:
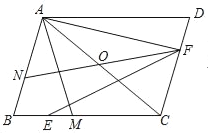
【题目】如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)若BM=4,MC=3,AC=![]() ,求AM的长度;
,求AM的长度;
(2)若∠ACB=45°,求证:AN+AF=![]() EF.
EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点A、C均在坐标轴上,且OA=4,OC=3,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;动点N从点C出发沿CB向终点B以同样的速度移动,当两个动点运动了x秒(0<x<4)时,过点N作NP⊥BC于点P,连接MP.

(1)直接写出点B的坐标,并求出点P的坐标(用含x的式子表示);
(2)设△OMP的面积为S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动的过程中,是否存在某一时刻,使△OMP是等腰三角形?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com