练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

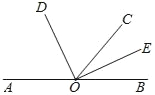
    【题目】如图，点 A，O，B 在同一条直线上，OD，OE 分别平分∠AOC 和∠BOC．

    (1)求∠DOE 的度数；

    (2)如果∠COD＝65°，求∠AOE 的度数．

    【答案】(1)90°；(2) 155°.

    【解析】

    （1）由已知条件和观察图形，再利用角平分线的定义和平角为180度即可求得∠DOE互余的度数；

    （2）由（1）可知∠BOE＝∠COE＝90°﹣∠COD＝25°，再由平角的定义即可得答案.

    （1）如图，∵OD 是∠AOC 的平分线，

    ∴∠COD＝∠AOC，

    ∵OE 是∠BOC 的平分线，

    ∴∠COE＝ ∠BOC，

    所以∠DOE＝∠COD+∠COE＝（∠AOC+∠BOC）＝ ∠AOB＝×180°=90°；

    （2）由（1）可知：

    ∠BOE＝∠COE＝90°﹣∠COD＝25°，

    所以∠AOE＝180°﹣∠BOE＝155°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，斜边AO=10，sin∠AOB= ，反比例函数 的图象经过AO的中点C，且与AB交于点D，则点D的坐标为 ．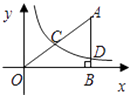

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列等式：（1）13＝×12×22；（2）13+23＝×22×32；（3）13+23+33＝×32×42；（4）13+23+33+43＝×42×52；

    根据上述等式的规律，解答下列问题：

    （1）写出第5个等式：_____；

    （2）写出第n个等式（用含有n的代数式表示）；

    （3）设s是正整数且s≥2，应用你发现的规律，化简：×s2×（s+1）2﹣×（s﹣1）2×s2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的平分线，CA2是∠A1CD的平分线，BA3是∠A2BD的平分线，CA3是∠A2CD的平分线．若∠A1＝α，则∠A2019＝________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程： （1）x﹣3＝-2x+1 （2）18（x-1）＝-2（2x﹣1）（3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】妈妈要榨果汁，她有苹果、橙子、雪梨三种水果，且其颗数比为 9：7：6， 她榨完果汁后，苹果、橙子、雪梨的颗数比变为 6：3：4，已知妈妈榨果汁时没有使用雪梨， 小明根据他的发现利用所学的数学知识推断出妈妈榨果汁时只使用了橙子，妈妈告诉小明他的推断是完全正确的。请你尝试写出小明的推断过程。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是某个正方体的表面展开图，各个面上分别标有1﹣6的不同数字，若将其折叠成正方体，则相交于同一个顶点的三个面上的数字之和最大的是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O（0，0），A（0，1）是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1 ， 再以正方形的对角线OA2作正方形OA1A2B1 ， …，依此规律，则点A2017的坐标是（ ）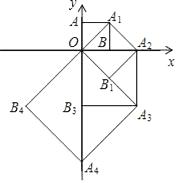

    A.（0，21008）
    B.（ ， ）
    C.（ ，0）
    D.（ ，- ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以直线AB上一点O为端点作射线OC，使∠BOC＝60°，将一个直角三角形的直角顶点放在点O处．（注：∠DOE＝90°）

    （1）如图1，若直角三角板DOE的一边OD放在射线OB上，则∠COE＝　 　°；

    （2）如图2，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OE恰好平分∠AOC，请说明OD所在射线是∠BOC的平分线；

    （3）如图3，将三角板DOE绕点O逆时针转动到某个位置时，若恰好∠COD＝∠AOE，求∠BOD的度数？

    查看答案和解析>>

    同步练习册答案