
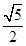 个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.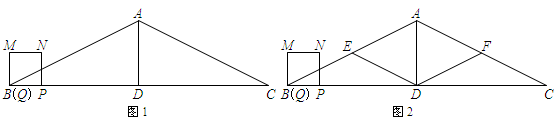
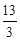
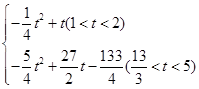
 ∴
∴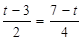 ∴t=
∴t=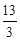 .(2)画出运动中的图形,根据具体图形利用未知数t的代数式表示并求其面积.(3)重点是准确画出图形变化,PN中点与G何时重合.
.(2)画出运动中的图形,根据具体图形利用未知数t的代数式表示并求其面积.(3)重点是准确画出图形变化,PN中点与G何时重合. ∴PN是△ABD的中位线 ∴BP=2∴t=1
∴PN是△ABD的中位线 ∴BP=2∴t=1 ∴
∴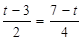 ∴t=
∴t=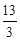 .
.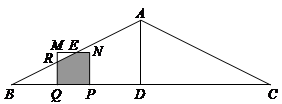
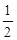 ME=
ME=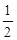 (2-t)∴S△MRE =
(2-t)∴S△MRE =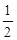 ME·MR=
ME·MR=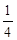 (2-t)2
(2-t)2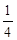 (2-t)2=-
(2-t)2=-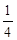 t2+t
t2+t 
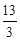 <t<5时
<t<5时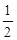 PC=
PC=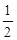 (7-t)
(7-t)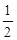 AM·MS=(5-t)2,S△PTC =
AM·MS=(5-t)2,S△PTC =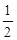 PC·PT=
PC·PT=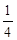 (7-t)2
(7-t)2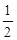 AD·CD=
AD·CD=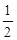 ×2×4=4
×2×4=4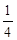 (7-t)2=-
(7-t)2=-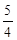 t2+
t2+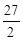 t-
t-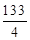
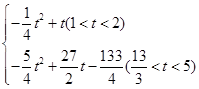
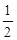 ,G为BE中点,也为NP中点.
,G为BE中点,也为NP中点.
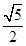 ×2=
×2= ,到达DE中点.正方形 PQEN运动到图形位置,EQ=1,GP=
,到达DE中点.正方形 PQEN运动到图形位置,EQ=1,GP=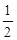 NP为NP中点.
NP为NP中点.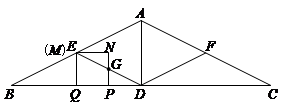
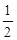 (t-3) 由勾股定理得DR=
(t-3) 由勾股定理得DR=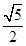 (t-3) 此时DG=
(t-3) 此时DG=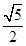 t-
t- =
=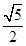 (t-3) 所以点R与点G重合.
(t-3) 所以点R与点G重合.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源:不详 题型:解答题
 与
与 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①
交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:① ;②
;②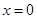 时,
时,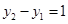 ;③平行于x轴的直线
;③平行于x轴的直线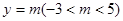 与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )
与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )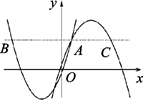
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
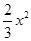 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn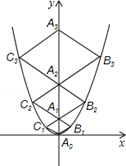
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=(x-2)2 | B.y=(x-2)2+6 | C.y=x2+6 | D.y=x2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题


查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com