
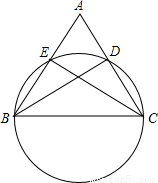
如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连结EC、BD.
(1)求证:ΔABD∽ΔACE;
(2)若ΔBEC与ΔBDC的面积相等,试判定三角形ABC的形状.
(1) 证明见解析(2) 等腰三角形
【解析】(1)证明:∵弧ED所对的圆周角相等,∴∠EBD=∠ECD,
又∵∠A=∠A,∴△ABD∽△ACE。
(2)解:△ABC为等腰三角形。理由如下:
∵S△BEC=S△BCD,S△ACE=S△ABC-S△BEC,S△ABD=S△ABC-S△BCD,
∴S△ACE=S△ABD。
又由(1)知△ABD∽△ACE,∴对应边之比等于1。
∴AB=AC,即△ABC为等腰三角形。
(1)利用圆周角定理得出∠EBD=∠ECD,再利用∠A=∠A,得出△ABD∽△ACE。
(2)根据△BEC与△BDC的面积相等,得出S△ACE=S△ABD,进而求出AB=AC,得出答案。


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
 (2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.
(2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.查看答案和解析>>
科目:初中数学 来源: 题型:
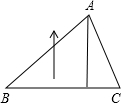 如图,三角形ABC的底边BC长3厘米,BC边上的高是2厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时,三角形扫过的面积是多少平方厘米( )
如图,三角形ABC的底边BC长3厘米,BC边上的高是2厘米,将三角形以每秒3厘米的速度沿高的方向向上移动2秒,这时,三角形扫过的面积是多少平方厘米( )| A、21 | B、19 | C、17 | D、15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com