
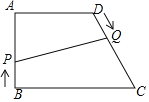
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=AD=8cm,CD=10cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为lcm/s.连接PQ,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,PQ∥AD?
(2)设四边形APQD的面积为y(cm2),求y与t的函数关系式;
(3)是否存在某一时刻t,使S四边形APQO:S四边形BCQP=17:27?若存在,求出t的值,并求此时PQ的长;若不存在,请说明理由.
【答案】(1)当t为![]() s时,PQ∥AD;(2)y与t的函数关系式是y=
s时,PQ∥AD;(2)y与t的函数关系式是y=![]() ;(3)t的值为2s或
;(3)t的值为2s或![]() s,此时PQ的长为
s,此时PQ的长为![]() cm,见解析.
cm,见解析.
【解析】
(1)根据平行线分线段成比例的性质解答即可;
(2)过点D作DE⊥BC于点E,过点Q作QF⊥AD交AD的延长线于F,根据矩形的性质和三角函数解答即可;
(3)过点Q作QH⊥AB于点H,根据四边形面积公式进行解答即可.
解:(1)∵PQ∥AD,AD∥BC
∴![]() ,
,
即![]()
解得,![]()
答:当t为![]() s时,PQ∥AD.
s时,PQ∥AD.
(2)过点D作DE⊥BC于点E,过点Q作QF⊥AD交AD的延长线于F
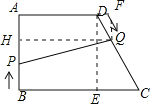
∴∠DEC=∠QFD=90°
∵AD∥BC,∠A=90°
∴∠ABC=180°-∠A=90°
∴四边形ABND是矩形
∴AB=DE,BE=AD
在Rt△DEC中,![]() ,
,
∵∠C=∠QDF
∴在Rt△DFQ和Rt△DEC中,
sin∠QDF=![]() ,即
,即![]()
∴![]()
cos∠QDF=![]() ,即
,即![]()
∴![]()
∵在四边形ABCD中,∠A=90°,AB=AD
∴∠ABD=∠ADB=45°
∴y=S四边形APQD=S四边形APQF-S△DQF
=![]()
=![]()
=![]()
答:y与t的函数关系式是y=![]() .
.
(3)若S四边形APQD:S四边形BCQP=17:27,则y=![]() S四边形ABCD
S四边形ABCD
∵S四边形ABCD=![]()
∴![]() =34
=34
解得t1=2,![]()
∴t的值为2s或![]() s.
s.
过点Q作QH⊥AB于点H,
∴PH=![]()
QH=AF=![]()
∴PQ=![]()
当t=2时,PQ=![]()
当t=![]() 时,PQ=
时,PQ=![]()
∴此时PQ的长为![]() cm.
cm.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
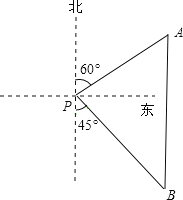
【题目】如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.
(1)求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?
(2)学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
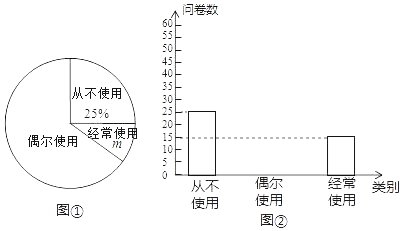
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,某校为了解学生对共享单车的使用情况,随机抽取部分学生进行问卷调查,并将这次调查的结果绘制了以下两幅不完整的统计图.
根据所给信息,解答下列问题:
(1)m= ;
(2)补全条形统计图;
(3)这次调查结果的众数是 ;
(4)已知全校共3000名学生,请估计“经常使用”共享单车的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )

A、3.25m B、4.25m C、4.45m D、4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.
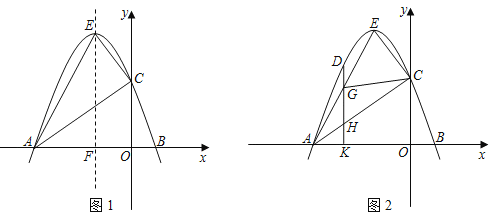
(1)请直接写出这条抛物线和直线AE、直线AC的解析式;
(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;
(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,
①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;
②在①的条件下,判断CG与AE的数量关系,并直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=﹣![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.图象经过点(1,﹣3)
B.图象分布在第一、三象限
C.图象关于原点对称
D.图象与坐标轴没有交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(材料阅读)
我们曾解决过课本中的这样一道题目:
如图1,四边形ABCD是正方形,E为BC边上一点,延长BA至F,使AF=CE,连接DE,DF.……
提炼1:△ECD绕点D顺时针旋转90°得到△FAD;
提炼2:△ECD≌△FAD;
提炼3:旋转、平移、轴对称是图形全等变换的三种方式.
(问题解决)
(1)如图2,四边形ABCD是正方形,E为BC边上一点,连接DE,将△CDE沿DE折叠,点C落在G处,EG交AB于点F,连接DF.
可得:∠EDF= °;AF,FE,EC三者间的数量关系是 .
(2)如图3,四边形ABCD的面积为8,AB=AD,∠DAB=∠BCD=90°,连接AC.求AC的长度.
(3)如图4,在△ABC中,∠ACB=90°,CA=CB,点D,E在边AB上,∠DCE=45°.写出AD,DE,EB间的数量关系,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com