
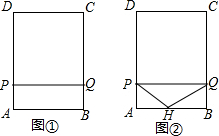
 如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).
如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).分析 (1)根据面积公式S△PCQ=$\frac{1}{2}$•QC•PQ计算即可.
(2)分四种情形①当0<t<4时②当4<t<7时③当7<t<11时④当11<t<14时,分别画出图形利用相似三角形的性质即可解决问题.
(3)利用配方法根据二次函数的最值问题解决即可.
(4)①当0<t<$\frac{9}{4}$时②当$\frac{9}{4}$≤t≤4时分别根据三种情形利用勾股定理列出方程解决.
解答 (1)解:t=2时,AP=3×2=6,
∵四边形ABCD 是矩形,
∴AD=BC=12,AB=CD=6,∠D=∠C=90°,
∵PQ⊥BC,
∴∠PQC=∠C=∠D=90°,
∴四边形CDPQ矩形,
∴PD=CQ=AD-AP=6,PQ=CD=9,
∴S△PCQ=$\frac{1}{2}$•QC•PQ=$\frac{1}{2}$×6×9=27.
故答案为27.
(2)①当0<t<4时,如图1中,
y=12-3t.
②当4<t<7时,如图2中,
∵∠APD+∠QPC=90°,∠QPC+∠PQC=90°,
∴∠APD=∠PQC,∵∠D=∠C=90°,
∴△APD∽△PQC,
∴$\frac{QC}{PD}$=$\frac{PC}{AD}$
∴$\frac{y}{3t-12}$=$\frac{21-3t}{12}$,
∴y=-$\frac{3}{4}$t2+$\frac{33}{4}$t-21.
③当7<t<11时,如图3中,
同理可证△PQC∽△APB,
∴$\frac{QC}{PB}$=$\frac{PC}{AB}$,
∴$\frac{y}{33-3t}$=$\frac{3t-21}{9}$,
∴y=-t2+18t-77.
④当11<t<14时,如图4中,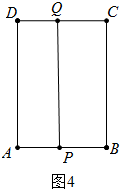
QC=PB,y=3t-33.
综上所述:y=$\left\{\begin{array}{l}{12-3t}&{(0<t<4)}\\{-\frac{3}{4}{t}^{2}+\frac{33}{4}t-21}&{(4<t<7)}\\{-{t}^{2}+18t-77}&{(7<t<11)}\\{3t-33}&{(11<t<14)}\end{array}\right.$.
(3)当点P在边CB上运动时,QC的长有最大值.
∵11<t<14,y=-t2+18t-77=-(t-9)2+4,
∴t=9时,y最大值=4.
(4)如图5中,
①当0<t<$\frac{9}{4}$时,∵PA=3t.AH=4t,HB=9-4t,
如果PH=HQ,那么AH=BH,4t=$\frac{9}{2}$,t=$\frac{9}{8}$,
如果PH=PQ=9,那么PH2=PA2+AH2,92=(3t)2+(4t)2,t=$\frac{9}{5}$,
如果PQ=QH,那么QH2=BH2+BQ2,92=(3t)2+(9-4t)2,t=$\frac{72}{25}$(不合题意舍弃).
当$\frac{9}{4}$≤t≤4时,BH=4t-9,AH=18-4t,
如果PH=HQ,那么AH=BH,4t=9+$\frac{9}{2}$,t=$\frac{27}{8}$,
如果PH=PQ=9,那么PH2=PA2+AH2,92=(3t)2+(18-4t)2,方程无解.
如果PQ=QH,那么QH2=BH2+BQ2,92=(3t)2+(4t-9)2,t=$\frac{72}{25}$.
综上所述t=$\frac{9}{8}$或$\frac{9}{5}$或$\frac{72}{25}$或$\frac{27}{8}$时,△PHQ是等腰三角形.
点评 本题考查四边形综合题、相似三角形的判定和性质、勾股定理、二次函数、分段函数等知识,解题的关键是学会分类讨论,需要正确画出图形,注意不能漏解,题目有点难度,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
 如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;
如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
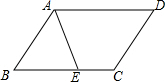 如图,已知?ABCD的周长为16cm,AE平分∠BAD交BC于E,设AB=xcm(0<x<4).
如图,已知?ABCD的周长为16cm,AE平分∠BAD交BC于E,设AB=xcm(0<x<4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
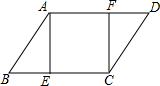 如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )
如图,在?ABCD中,∠B=60°,AB=12,AE⊥BC于点E,CF⊥AD于点F,若四边形AECF是正方形,则四边形AECF的周长为( )| A. | 18 | B. | 24$\sqrt{2}$ | C. | 24 | D. | 24$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{{x}^{2}}$ | C. | $\sqrt{0.7}$ | D. | $\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com