
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1 , y1)、P2(x2 , y2),其两点间的距离 ![]() ,
,
同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.
【答案】
(1)解:∵A(2,4)、B(﹣3,﹣8),
∴AB= ![]() =13
=13
(2)解:∵A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,
∴AB=|4﹣(﹣1)|=5
(3)解:△DEF为等腰三角形,理由为:
∵D(1,6)、E(﹣2,2)、F(4,2),
∴DE= ![]() =5,DF=
=5,DF= ![]() =5,EF=
=5,EF= ![]() =6,即DE=DF,
=6,即DE=DF,
则△DEF为等腰三角形
(4)解:做出F关于x轴的对称点F′,连接DF′,与x轴交于点P,此时DP+PF最短,

设直线DF′解析式为y=kx+b,
将D(1,6),F′(4,﹣2)代入得: ![]() ,
,
解得:  ,
,
∴直线DF′解析式为y=﹣ ![]() x+
x+ ![]() ,
,
令y=0,得:x= ![]() ,即P(
,即P( ![]() ,0),
,0),
∵PF=PF′,
∴PD+PF=DP+PF′=DF′= ![]() =
= ![]() ,
,
则PD+PF的长度最短时点P的坐标为( ![]() ,0),此时PD+PF的最短长度为
,0),此时PD+PF的最短长度为 ![]() .
.
【解析】(1)代入公式易得AB=![]() =13。
=13。
(2)由于A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,有公式易得AB=|4﹣(﹣1)|=5;
(3)由三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2)代入公式可得各点之间的距离,再利用勾股定理的逆定理可得三角形为直角三角形;
(4)做出F关于x轴的对称点F′,连接DF′,与x轴交于点P,此时DP+PF最短,求得直线DF′解析式可得P点坐标,再利用公式可得PD+PF的最短长度为 ![]()
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°.若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)( )

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北.据统计,2016年“快的打车”账户流水总金额达到147.3亿用科学记数法表示为( )
A.1.473×1010
B.14.73×1010
C.1.473×1011
D.1.473×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
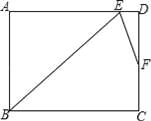
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
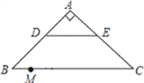
【题目】如图,在Rt△ABC中.∠A=90°.AB=AC,BC=20,DE是△ABC的中位线.点M是边BC上一点.BM=3.点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有2cm,3cm,5cm,7cm长的四条线段,任取其中三条,可以组成的三角形的情况个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com