
分析 (1)加4再减4,化成完全平方,得y=(x-2)2-3,分别写出对称轴,顶点坐标和最小值;
(2)由根据与系数的关系先计算:x1+x2=4,x1x2=1,再将x12+x22进行变形为(x1+x2)2-2x1x2,代入计算即可.
解答 解:(1)∵y=x2-4x+1=x2-4x+4-4+1=(x-2)2-3,
∴当x=2时,y最小值=3,
对称轴为x=2,顶点为(2,-3);
(2)由题意,x1,x2是方程x2-4x+1=0的两根,
∴x1+x2=4,x1x2=1,
∴x12+x22=(x1+x2)2-2x1x2=42-2×1=14.
点评 本题考查了二次函数的性质和抛物线与x轴的交点问题,利用顶点式可以表示二次函数的对称轴、顶点坐标和最值:二次函数y=a(x-h)2+k中,①当a>0时,对称轴是直线x=h,顶点坐标为(h,k),因为图象有最低点,所以函数有最小值,当x=h时,y有最小值是k;②当a<0时,对称轴是直线x=h,顶点坐标为(h,k),因为图象有最高点,所以函数有最大值,当x=h时,y有最大值是k;求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标;反之,知道交点坐标,可由根与系数关系计算代数式的值,如第(2)问.


科目:初中数学 来源: 题型:解答题
| 进货价/(元/箱) | 出售加价率 | |
| A种酸奶 | 16 | 20% |
| B种酸奶 | 20 | 25% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
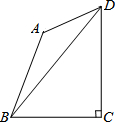 如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.
如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
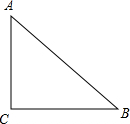 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,现有一点O从点A出发,沿AB方向运动,当到达点B时,运动停止,以点O为圆心,r为半径的圆记为⊙O.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,现有一点O从点A出发,沿AB方向运动,当到达点B时,运动停止,以点O为圆心,r为半径的圆记为⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com