
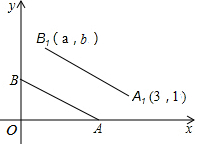
 如图所示,A、B的坐标分别为(2,0),(0,1),且线段A1B1=AB,A1B1∥AB.若A1、B1的坐标分别为(3,1),(a,b),则a+b的值为( )
如图所示,A、B的坐标分别为(2,0),(0,1),且线段A1B1=AB,A1B1∥AB.若A1、B1的坐标分别为(3,1),(a,b),则a+b的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
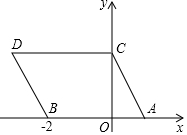 如图,在平面直角坐标系中,点A、B的坐标分别为(1,0)、(-2,0),现同时将点A、B分别向上平移2个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、CD.
如图,在平面直角坐标系中,点A、B的坐标分别为(1,0)、(-2,0),现同时将点A、B分别向上平移2个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
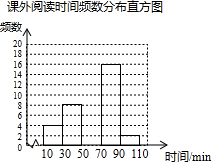 某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.
某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.| 课外阅读时间t | 频数 | 百分比 |
| 10≤t<30 | 4 | 8% |
| 30≤t<50 | 8 | 16% |
| 50≤t<70 | a | 40% |
| 70≤t<90 | 16 | b |
| 90≤t<110 | 2 | 4% |
| 合计 | 50 | 100% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com