
分析 (1)根据D、E分别为CO、AB的中点,判断出DE∥OA,即可判断出Q是CP的中点,所以Q为Rt△COP的外心,据此解答即可.
(2)首先求出y=$\frac{3}{4}$x和y=$-\frac{4}{3}$x+$\frac{25}{3}$的交点A的坐标,然后根据勾股定理,求出正方形的边长是多少即可.
(3)首先作AM⊥x轴于点M,PN⊥x轴于点N,判断出E为AB与⊙Q相切的切点;然后根据AE和AO分别是⊙Q的切线与割线,可得AE2=AP•AO,据此求出AP、OP的长度各是多少;然后根据AM∥PN,求出ON,PN的长度,即可求出点P坐标是多少.
解答 (1)证明:如图1,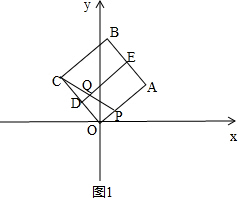 ,
,
∵D、E分别为CO、AB的中点,
∴DE∥OA,
∴Q是CP的中点,
又∵△COP为直角三角形,
∴Q为△COP的外心.
(2)解:如图2,作AM⊥x轴于点M,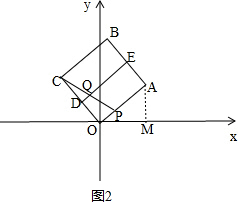 ,
,
由$\left\{\begin{array}{l}{y=\frac{3}{4}x}\\{y=-\frac{4}{3}x+\frac{25}{3}}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$
∴点A的坐标为(4,3),
∴OA=$\sqrt{{OM}^{2}{+AM}^{2}}=\sqrt{{4}^{2}{+3}^{2}}=5$,
即正方形的边长是5.
(3)解:如图3,作AM⊥x轴于点M,PN⊥x轴于点N,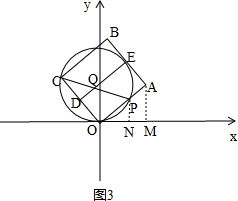 ,
,
当AB与⊙Q相切时,
∵圆心Q在直线DE上,DE⊥AB,
∴E为AB与⊙Q相切时的切点,
又∵AE和AO分别是⊙Q的切线与割线,
∴AE2=AP•AO,
∵AE=$\frac{1}{2}AB=\frac{1}{2}×5=\frac{5}{2}$,AO=5,
∴AP=${(\frac{5}{2})}^{2}$$÷5=\frac{25}{4}÷5=\frac{5}{4}$,OP=5-$\frac{5}{4}=\frac{15}{4}$,
∵AM⊥x轴,PN⊥x轴,
∴AM∥PN,
∴$\frac{PN}{AM}=\frac{ON}{OM}=\frac{OP}{AP}$,
即$\frac{PN}{3}=\frac{ON}{4}=\frac{\frac{15}{4}}{5}$,
解得ON=3,PN=$\frac{9}{4}$,
∴AB与⊙Q相切时点P坐标是(3,$\frac{9}{4}$).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了正方形的性质和应用,圆的切线和割线的性质和应用,以及勾股定理的应用,要熟练掌握.


科目:初中数学 来源: 题型:选择题
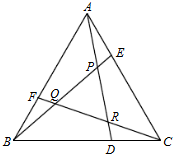 如图所示,已知△ABC面积为l,点D、E、F分别在BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD、BE、CF两两相交于P、Q、R,则△PQR的面积为( )
如图所示,已知△ABC面积为l,点D、E、F分别在BC、CA、AB上,且BD=2DC,CE=2EA,AF=2FB,AD、BE、CF两两相交于P、Q、R,则△PQR的面积为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{14}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | -9 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
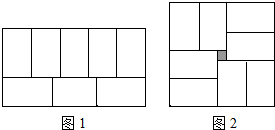 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )| A. | 120mm2 | B. | 135mm2 | C. | 108mm2 | D. | 96mm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com