Question

12．△ABC是等边三角形，点A与点D的坐标分别是A（4，0），D（10，0）．
（1）如图1，当点C与点O重合时，求直线BD的解析式；
（2）如图2，点C从点O沿y轴向下移动，当以点B为圆心，AB为半径的⊙B与y轴相切（切点为C）时，求点B的坐标；
（3）如图3，点C从点O沿y轴向下移动，过点B作BQ⊥x轴，垂足为Q，当点C的坐标为C（0，-2$\sqrt{3}$）时，求$\frac{BQ}{DQ}$的值．

Answer 1

分析 （1）首先求出点B的坐标是多少，然后设直线BD的解析式为y=kx+b，根据点B、D的坐标，求出k、b的值，即可确定出直线BD的解析式．
（2）首先作BE⊥x轴于点E，根据以AB为半径的⊙B与y轴相切于点C，判断出∠OCB=90°，再根据△ABC是等边三角形，推得∠ACO=30°，所以AC=2OA；然后根据A（4，0），可得OA=4，应用勾股定理，求出点B的坐标是多少即可．
（3）首先以点B为圆心，AB为半径作⊙B，交y轴于点C、E，过点B作BF⊥CE于F，连接AE，在Rt△AOE中，根据勾股定理，求出OE的值是多少；然后在Rt△CFB中，由勾股定理，求出BF的值是多少；最后根据BQ⊥x轴于点Q，分别求出BQ、OQ的值各是多少，再根据OD=10，求出DQ的值，即可求出$\frac{BQ}{DQ}$的值是多少．

解答 解：（1）如图1，，
∵A（4，0），
∴OA=4，
∴等边三角形ABC的高为：4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，
∴B（2，-2$\sqrt{3}$）．
设直线BD的解析式为y=kx+b，由题意，得
$\left\{\begin{array}{l}{2k+b=-2\sqrt{3}}\\{10k+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{4}}\\{b=-\frac{5\sqrt{3}}{2}}\end{array}\right.$，
∴直线BD的解析式为：y=$\frac{\sqrt{3}}{4}$x-$\frac{5\sqrt{3}}{2}$．

（2）如图2，作BE⊥x轴于点E，，
∵BE⊥x轴，
∴∠AEB=90°．
∵以AB为半径的⊙B与y轴相切于点C，
∴BC⊥y轴，
∴∠OCB=90°．
∵△ABC是等边三角形，
∴∠ACB=60°，
∴∠ACO=90°-60°=30°，
∴AC=2OA．
∵A（4，0），
∴OA=4，
∴AC=8，
∴OC=$\sqrt{{AC}^{2}{-OA}^{2}}=\sqrt{{8}^{2}{-4}^{2}}=4\sqrt{3}$．
∵AE=OA=4，
∴OE=8，
∴B（8，-4$\sqrt{3}$）．

（3）如图3，以点B为圆心，AB为半径作⊙B，交y轴于点C、E，过点B作BF⊥CE于F，连接AE，，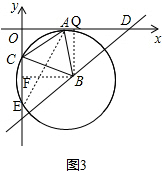
∵△ABC是等边三角形，
∴AC=BC=AB，∠ABC=∠ACB=∠BAC=60°，
∴∠OEA=$\frac{1}{2}$∠ABC=$\frac{1}{2}×60°$=30°，
∴AE=2OA．
∵A（4，0），
∴OA=4，
∴AE=8，
∴OE=$\sqrt{{AE}^{2}{-OA}^{2}}$=$\sqrt{{8}^{2}{-4}^{2}}$=4$\sqrt{3}$．
∵C（0，-2$\sqrt{3}$），
∴OC=2$\sqrt{3}$，
∴AC=$\sqrt{{OA}^{2}{+OC}^{2}}=\sqrt{{4}^{2}{+（2\sqrt{3}）}^{2}}$=2$\sqrt{7}$，
∴CE=OE-OC=4$\sqrt{3}-2\sqrt{3}$=2$\sqrt{3}$．
∵BF⊥CE，
∴CF=$\frac{1}{2}$CE=$\frac{1}{2}×2\sqrt{3}$=$\sqrt{3}$，
∴OF=OC+CF=2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$．
在Rt△CFB中，由勾股定理，可得
BF²=BC²-CF²=${（2\sqrt{7}）}^{2}$-${（\sqrt{3}）}^{2}$=28-3=25，
∴BF=5，
∴B（5，-3$\sqrt{3}$）．
∵BQ⊥x轴于点Q，
∴BQ=OF=3$\sqrt{3}$，OQ=BF=5，
∵D（10，0），
∴OD=10，
∴DQ=OD-OQ=10-5=5，
∴tan∠ODB=$\frac{BQ}{DQ}$=$\frac{3\sqrt{3}}{5}$．

点评 （1）此题主要考查了一次函数综合题，考查了分析推理能力，考查了数形结合思想的应用，考查了从已知函数图象中获取信息，并能利用获取的信息解答相应的问题的能力．
（2）此题还考查了直线解析式的求法，以及勾股定理的应用等，要熟练掌握，解答此题的关键是辅助线的灵活应用．