
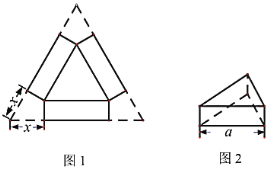
【题目】如图1,小明用一张边长为![]() 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为![]() ,再折成如图2所示的无盖糖果盒,它的容积记为
,再折成如图2所示的无盖糖果盒,它的容积记为![]() .
.
(1)![]() 关于
关于![]() 的函数关系式是__________,自变量
的函数关系式是__________,自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 3.125 | ________ | 3.375 | ________ | 0.625 | 0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

(3)利用函数图象解决:
①该糖果盒的最大容积是__________;
②若该糖果盒的容积超过![]() ,请估计糖果盒的底边长
,请估计糖果盒的底边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)
【答案】(1)(1)![]() ,
,![]() ;(2)①表格见解析;②描点见解析;③连线见解析;(3)①4;②
;(2)①表格见解析;②描点见解析;③连线见解析;(3)①4;②![]() .
.
【解析】
(1)根据正三棱柱的体积公式可以列出y关于x的函数表达式,根据x的实际意义可直接分析出其取值范围;
(2)①分别将x=1和2代入函数关系式可求出y的值;②根据表内数据可在平面直角坐标系上描点;③可直接用平滑曲线连接;
(3)根据图象即可得到结论.
解:(1)∵无盖糖果盒的高为![]() ,a=6-2x,
,a=6-2x,
∴底面正三角形的面积为![]() ,
,
![]() ,
,
故答案为:y=x(3-x)2,0<x<3;
(2)①列表:补充表格中的数据;
x | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
y | 4 | 2 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;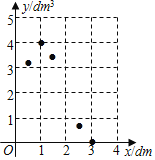
③连线:用光滑的曲线顺次连接各点.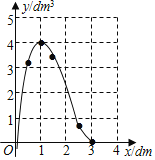
(3)①该糖果盒的最大容积是4;
②由图象可知:0.27<x<2,
因为a=6-2x,
所以2<a<5.5.
故答案为:4;2<a<5.5.
【点晴】
本题考查了二次函数的应用,函数的性质,画函数图象的步骤列表、描点、连线,以及数形结合思想的运用等,解题关键是要熟练掌握函数的定义及数形结合的思想.


科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
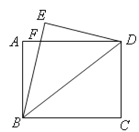
(1)求证:△BDF是等腰三角形;
(2)若AB=6,AD=8,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是同-种蔬菜的两种裁植方法.甲:![]() 四珠顺次连结成为一个菱形,且
四珠顺次连结成为一个菱形,且![]() .乙:
.乙:![]() 四株连结成一个正方形。其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距:设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积。设株距都为
四株连结成一个正方形。其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距:设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积。设株距都为![]() ,其它客观因素都相同.则对于下列说法:
,其它客观因素都相同.则对于下列说法:
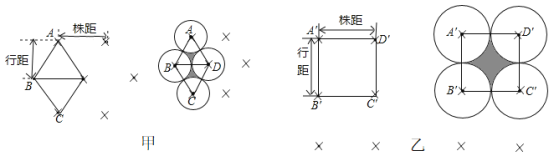
①甲的行距比乙的小;②甲的行距为![]() ;③甲、乙两种栽植方式,蔬菜形成的影子面积相同;④甲的空隙地面积比乙的空隙地面积少
;③甲、乙两种栽植方式,蔬菜形成的影子面积相同;④甲的空隙地面积比乙的空隙地面积少![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() 三个数所对应的点分别为
三个数所对应的点分别为![]() ,已知
,已知![]() ,且
,且![]() 的倒数是它本身,且
的倒数是它本身,且![]() 满足
满足![]() .
.
![]()
(1)求代数式![]() 的值:
的值:
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则与点
重合,则与点![]() 重合的点表示的数是_______;
重合的点表示的数是_______;
(3)请在数轴上确定一点![]() ,使得
,使得![]() ,则点
,则点![]() 表示的数是______.
表示的数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
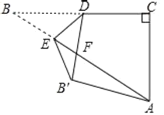
【题目】如图,在Rt△ABC中,∠C=90°,BC=4![]() ,AC=4,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若∠AB′F为直角,则AE的长为__________.
,AC=4,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若∠AB′F为直角,则AE的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
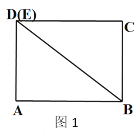
【题目】在综合与实践课上,老师组织同学们以“三角形纸片的旋转”为主题开展数学活动.如图1,现有矩形纸片ABCD,AB=8cm,AD=6cm.连接BD,将矩形ABCD沿BD剪开,得到△ABD和△BCE.保持△ABD位置不变,将△BCE从图1的位置开始,绕点B按逆时针方向旋转,旋转角为α(0°≤α<360°).在△BCE旋转过程中,边CE与边AB交于点F.
(1)如图2,将图1中的△BCE旋转到点C落在边BD上时,CF= ;
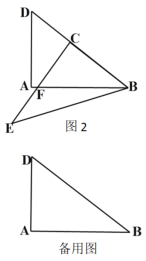
(2)继续旋转△BCE,当点E落在DA延长线上时,求出CF的长;
(3)在△BCE旋转过程中,连接AE,AC,当AC=AE时,直接写出此时α的度数及△AEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
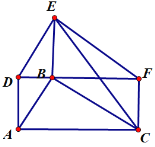
【题目】如图,△DEF由△ABC平移得到,∠DFE=∠CDF=30°,∠DEF=90°,BE⊥DF于点B.连接CE,AB=3.
(1)求证:四边形ACDF为矩形
(2)求线段CE的长和△CEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com