
【题目】如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.

(1)请写出图中全等三角形(不再添加辅助线).
(2)求证:△ABE≌△CDF;
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据全等三角形的判定定理SSS(三条边分别对应相等的两个三角形全等),SAS(两边及其夹角分别对应相等的两个三角形全等)判定图中的全等三角形;
(2)根据平行四边形的性质得到AB=CD,AB∥CD,推出∠BAE=∠FCD,根据垂直的定义得到∠AEB=∠CFD=90°,根据AAS(两角及其中一个角的对边对应相等的两个三角形全等)即可得到答案.
解:(1)①△ABC≌△CDA(SSS);②△BCE≌△DAF(SAS);③△ABE≌△CDF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠FCD,
又∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS).


科目:初中数学 来源: 题型:
【题目】如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.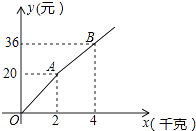
A.6
B.8
C.9
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实验课上,王老师让大家用矩形纸片折出菱形.小华同学的操作步骤是:
(1)如图①,将矩形ABCD沿着对角线BD折叠;
(2)如图②,将图①中的△A’BF沿BF折叠得到△A’’BF;
(3)如图③,将图②中的△CDF沿DF折叠得到△C’DF;
(4)将图③展开得到图④,其中BD、BE、DF为折叠过程中产生的折痕.

试解答下列问题:
(1)证明图④中的四边形BEDF为菱形;
(2)在图④中,若BC=8,CD=4,求菱形BEDF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京某中学为了迎接世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:

请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整:
(3)若测试成绩不低于90分的同学可以获得世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”?
查看答案和解析>>
科目:初中数学 来源: 题型:
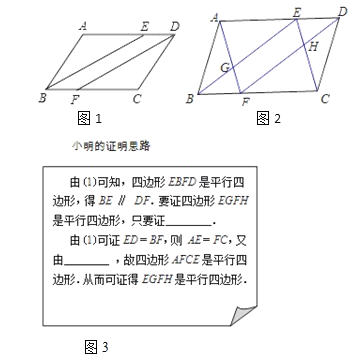
【题目】如图1,ABCD中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)如图2,小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图3)中补全他的证明思路,再在答题纸上写出规范的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿AB方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形?
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题一:如图①,已知AC=160km,甲,乙两人分别从相距30km的A,B两地同时出发到C地.若甲的速度为80km/h,乙的速度为60km/h,设乙行驶时间为x(h),两车之间距离为y(km).
(1)当甲追上乙时,x= .
(2)请用x的代数式表示y.
问题二:如图②,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(3)分针OD指向圆周上的点的速度为每分钟转动 km,时针OE指向圆周上的点的速度为每分钟转动 °;
(4)若从2:00起计时,求几分钟后分针与时针第一次重合?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若x,y都是实数,且y=![]() +
+![]() +8,求5x+13y+6的值;
+8,求5x+13y+6的值;
(2)已知△ABC的三边长分别为a,b,c,且满足![]() +b2-6b+9=0,求c的取值范围。
+b2-6b+9=0,求c的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一题作答,若多选,则按所选的第一题计分.
A.正五边形的一个外角的度数是 .
B.比较大小:2tan71° ![]() (填“>”、“=”或“<”)
(填“>”、“=”或“<”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com