【题目】已知二次函数
的图象如图所示，给出以下结论：①
；②
；③
；④
，其中结论正确有（ ）个．
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断即可．
①由图知：抛物线与x轴有两个不同的交点,则△=b24ac>0，
即b2>4ac，故①正确；
②抛物线开口向上，得：a>0；
抛物线的对称轴为x=
=1，b=2a，故b<0；
抛物线交y轴于负半轴，得：c<0；
所以abc>0；故②正确；
③抛物线的对称轴为x==1，即b=2a，
故2a+b=0，故③错误；
④根据抛物线的对称轴方程可知：(1,0)关于对称轴的对称点是(3,0)；
当x=1时，y<0，所以当x=3时，也有y<0，即9a+3b+c<0；
故④正确；
所以这结论正确的有①②④.
故答案选B.
科目：初中数学 来源： 题型：
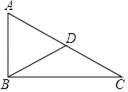
【题目】如图，在△ABC中，∠ABC=90°，BD为AC边上的中线．
（1）按如下要求尺规作图，保留作图痕迹，标注相应的字母：过点C作直线CE，使CE⊥BC于点C，交BD的延长线于点E，连接AE；
（2）求证：四边形ABCE是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把长方形OABC放在如图所示的平面直角坐标系中，点F、E分别在边OA和AB上，若点F （0，3），点C （9，0），且∠FEC＝90°，EF＝EC，则点E的坐标为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某茶叶公司经销一种茶叶，每千克成本为
元，市场调查发现在一段时间内，销量
（千克）随销售单价
（元/千克）的变化而变化，具有关系为：
，物价部门规定每千克的利润不得超过
元．设这种茶叶在这段时间内的销售利润
（元），解答下列问题：
求与的关系式；
当取何值时，的值最大？并求出最大值；
当销售利润的值最大时，销售额也是最大吗？判断并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】等腰Rt△ACB，∠ACB＝90°，AC＝BC，点A、C分别在x轴、y轴的正半轴上．
（1）如图1，求证：∠BCO＝∠CAO
（2）如图2，若OA＝5，OC＝2，求B点的坐标
（3）如图3，点C（0，3），Q、A两点均在x轴上，且S△CQA＝18．分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM，连接MN交y轴于P点，OP的长度是否发生改变？若不变，求出OP的值；若变化，求OP的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）a3aa2﹣9a2a4
（2）﹣m2（﹣m2）4（﹣m）3
（3）（﹣8）2018×（﹣0.125）2017
（4）（﹣
a2b﹣2ab2+
）（﹣9a）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，函数y＝
（k≠0，x＞0）的图象经过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线BC交函数y＝（k≠0，x＞0）的图象于点B．
（1）求k的值及点B的坐标
（2）在平面内存在点D，使得以A、B、C、D为顶点的四边形是平行四边形，直接写出符合条件的所有点D的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
