
����Ŀ���Կ�չ��ѧ��ÿ�����1Сʱ���������ij��ѧ����ѧУʵ���������������A����ӣ�B������C���ܲ���D�����������˶���Ŀ��Ϊ���˽�ѧ����ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼͳ��ͼ������ͼ����Ϣ����������⣺
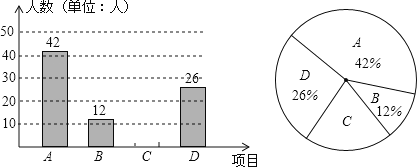
��1����У���ε����У��������˶�����ѧ����
��2���뽫����ͳ��ͼ����������
��3���ڱ��ε����ѧ���������ȡ1�ˣ���ϲ�����ܲ����ĸ����ж��
���𰸡���1��100����2����������3��![]()
�⣺��1����У����һ��������42��42��=100��ѧ����
��2����ϲ���ܲ�������=100��42��12��26=20���ˣ���
ϲ���ܲ�������ռ������ѧ�����İٷֱ�=![]() 100��=20����
100��=20����
�� ������ͳ��ͼ�����������£�

��3���ڱ��ε����������ȡһ��ѧ������ϲ���ܲ��ĸ���=![]() ��
��
����������1���������ͳ��ͼ������ͳ��ͼ������A��Ƶ��42����A��Ƶ��42%�����ɵõ���У���ε����У��������˶�����ѧ����
��2�����ã�1����������������ȥA��B��D���Ƶ�����ɣ�C��Ƶ������100���ɵõ�C��Ƶ�ʣ��Ӷ�������ͳ��ͼ����������
��3����ָ��ʹ�ʽֱ�ӽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AOB�У�OA=10����AOB=36�㣮�����������Ƶ�B˳ʱ����ת����һ������A��O��B������A����O��B�ϣ����O���˶�·����Ϊcm������������У� 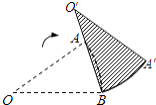
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
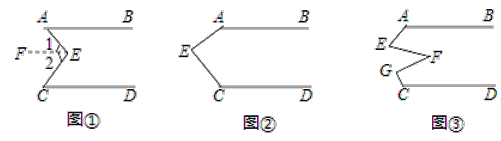
����Ŀ������֪����ͼ����AB��CD����E��ֱ��AB��CD֮�䣬����AE��BE����˵����BEE+��DCE����AEC����������������Ľ�����̣����������Ľ�����̣�����գ����ɻ���ѧʽ����
�⣺��ͼ�٣�����E��EF��AB
���BAE����1���� ����
��AB��CD���� ����
��CD��EF���� ����
���2����DCE
���BAE+��DCE����1+��2���� ����
���BAE+��DCE����AEC
��̽��������E����ͼ�ڵ�λ��ʱ�������������䣬��˵����AEC+��FGC+��DCE��360�㣻
��Ӧ�ã���E��F��G��ֱ��AB��CD֮�䣬����AE��EF��FG��CG�������������䣬��ͼ�ۣ�����EFG��36�������BAE+��AEF+��FGC+��DCG���� ���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.a3��a2=a3?a��2
B.![]()
C.2a2+a2=3a4
D.��a��b��2=a2��b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABCΪֱ�������Σ��ֱ���ֱ�DZ�AC��BCΪֱ������ԲAmC��BnC����ABΪֱ������ԲACB����������������Ӱ���ֵ����֮��ΪS1����ABC�����ΪS2����S1��S2�Ĵ�С��ϵΪ��������

A. S1��S2 B. S1��S2 C. S1=S2 D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���Ӫij��Ʒ�Ƶ���ߣ�����ʱ�ĵ�����30Ԫ�������г����飺��һ��ʱ���ڣ����۵�����40Ԫʱ����������600���������۵���ÿ��1Ԫ���ͻ����۳�10����ߣ�
��1�����������Ʒ����ߵ����۵���ΪxԪ��x��40��������ֱ���x�Ĵ���ʽ����ʾ������y�������۸�Ʒ����������wԪ�����ѽ����д�ڱ����У�
���۵��ۣ�Ԫ�� | x |
������y������ | |
������������w��Ԫ�� |
��2���ڣ�1���������£����̳������10000Ԫ�����������������۵���xӦ��Ϊ����Ԫ��
��3���ڣ�1���������£�����߳��涨��Ʒ��������۵��۲�����44Ԫ�����̳�Ҫ��ɲ�����540���������������̳����۸�Ʒ�����õ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijУΪ�˴�������У��ȥ�깺��һ��ͼ�飮���˽⣬������ĵ��۱���ѧ��ĵ��۶�4Ԫ����12000Ԫ�����Ŀ���������8000Ԫ��������ѧ�鱾����ȣ�������ѧ��Ϳ�����ĵ�����ȥ����ȱ��ֲ��䣬��У������10000Ԫ�ٹ���һ����ѧ��Ϳ����飬�ʹ�����ѧ��550��������ܹ������ٱ������飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ��һ����ѧ������֪��������ʽA��B��B��3x2y��5xy��x��7������A��B����λͬѧ��A��B����A��B���������Ĵ�Ϊ6x2y��12xy��2x��9��
��1����������λͬѧ�������ȷ����
��2����xȡ������ֵ��A��3B��ֵ��һ����ֵ����y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һԲ��ˮ�ܵĽ���ͼ����֪��O�İ뾶OA=13��ˮ���AB=24����ˮ�����CD�� �� 
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com