
【题目】如图,AC为圆O的直径,弦AD的延长线与过点C的切线交于点B,E为BC中点,AC= ![]() ,BC=4.
,BC=4.
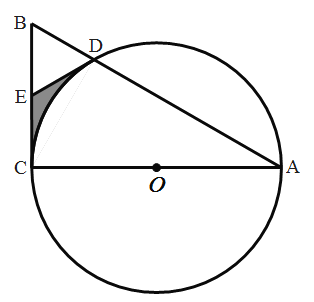
(1)求证:DE为圆O的切线;
(2)求阴影部分面积.
【答案】(1)证明见解析;(2)S阴影=4![]() -2π
-2π
【解析】
(1)根据斜边中线等于斜边一半得到DE=CE,再利用切线的性质得到∠BCO=90°,最后利用等量代换即可证明,(2)根据S阴影=2S△ECO-S扇形COD即可求解.
(1)连接DC、DO.
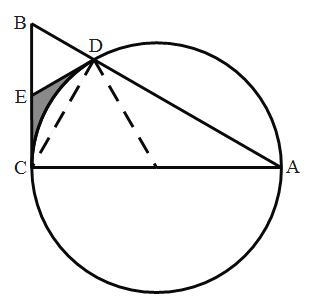
因为AC为圆O直径,
所以∠ADC=90°,则∠BDC=90°,
因为E为Rt△BDC斜边BC中点,
所以DE=CE=BE=![]() BC,
BC,
所以∠DCE=∠EDC,
因为OD=OC,
所以∠DCO=∠CDO.
因为BC为圆O 切线,
所以BC⊥AC,即∠BCO=90°,
所以∠ODE=∠ODC+∠EDC=∠OCD+∠DCE=∠BCO=90°,
所以ED⊥OD,
所以DE为圆O的切线.
(2)S阴影=2S△ECO-S扇形COD=4![]() -2π
-2π


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②3a+c>0;
③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
④当y>3时,x的取值范围是0≤x<2;
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
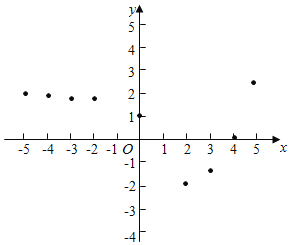
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .
查看答案和解析>>
科目:初中数学 来源: 题型:
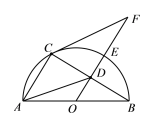
【题目】如图,AB是半圆O的直径,D为弦BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC,
(1)求证:CF为⊙O的切线;
(2)若四边形ACFD是平行四边形,求sin∠BAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
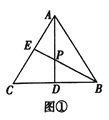
【题目】[问题发现]
如图①,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,则
,则![]() _____ ;
_____ ;
[拓展提高]
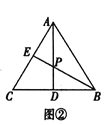
如图②,在等边三角形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,直线
上,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
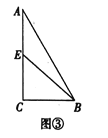
[解决问题]
如图③,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() .请直接写出
.请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,4),B(4,4),C(6,0).
(1)△ABC的面积是 .
(2)请以原点O为位似中心,画出△A'B'C',使它与△ABC的相似比为1:2,变换后点A、B的对应点分别为点A'、B',点B'在第一象限;
(3)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P' 的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
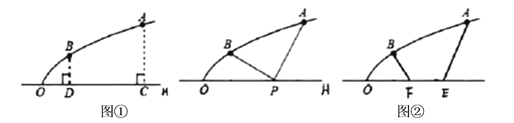
【题目】如图1,是一建筑物造型的纵截面,曲线![]() 是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线
是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线![]() ,
,![]() ,
,![]() 是与水平线
是与水平线![]() 垂直的两根支柱,
垂直的两根支柱,![]() 米,
米,![]() 米,
米,![]() 米.
米.
(1)如图1,为了安全美观,准备拆除支柱![]() 、
、![]() ,在水平线
,在水平线![]() 上另找一点
上另找一点![]() 作为地面上的支撑点,用固定材料连接
作为地面上的支撑点,用固定材料连接![]() 、
、![]() ,对抛物线造型进行支撑加固,用料最省时点
,对抛物线造型进行支撑加固,用料最省时点![]() ,
,![]() 之间的距离是_________.
之间的距离是_________.
(2)如图2,在水平线![]() 上增添一张
上增添一张![]() 米长的椅子
米长的椅子![]() (
(![]() 在
在![]() 右侧),用固定材料连接
右侧),用固定材料连接![]() 、
、![]() ,对抛物线造型进行支撑加固,用料最省时点
,对抛物线造型进行支撑加固,用料最省时点![]() ,
,![]() 之间的距离是_______________.
之间的距离是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像与x轴相交于点A,与y轴相交于点B,二次函数
的图像与x轴相交于点A,与y轴相交于点B,二次函数![]() 图像经过点A、B,与x轴相交于另一点C.
图像经过点A、B,与x轴相交于另一点C.
(1)求a、b的值;
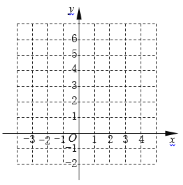
(2)在直角坐标系中画出该二次函数的图像;
(3)求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
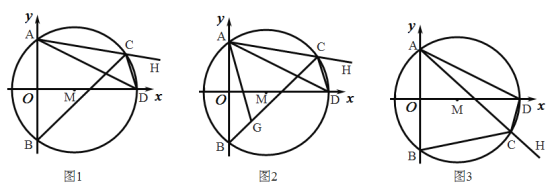
【题目】如图1,在平面直角坐标系中,已知![]() 的半径为5,圆心
的半径为5,圆心![]() 的坐标为
的坐标为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是
是![]() 上的一点(不与点
上的一点(不与点![]() 、
、![]() 、
、![]() 重合),连结
重合),连结![]() 并延长,连结
并延长,连结![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)当点![]() 在
在![]() 上时.
上时.
①求证:![]() ;
;
②如图2,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连结
,连结![]() .求证:
.求证:![]() ;
;
(3)如图3,当点![]() 在
在![]() 上运动的过程中,试探究
上运动的过程中,试探究![]() 的值是否发生变化?若不变,请直接写出该定值;若变化,请说明理由.
的值是否发生变化?若不变,请直接写出该定值;若变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com