
【题目】(1)操作发现:
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决:
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求:
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
【答案】(1)同意,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求简单的线段相等,可证线段所在的三角形全等,即连接EF,证△EGF≌△EDF即可;
(2)可设DF=x,BC=y;进而可用x表示出DC、AB的长,根据折叠的性质知AB=BG,即可得到BG的表达式,由(1)证得GF=DF,那么GF=x,由此可求出BF的表达式,进而可在Rt△BFC中,根据勾股定理求出x、y的比例关系,即可得到![]() 的值;
的值;
(3)方法同(2).
试题解析:(1)同意,连接EF,
则根据翻折不变性得,
∠EGF=∠D=90°,EG=AE=ED,EF=EF,
在Rt△EGF和Rt△EDF中,
![]()
∴Rt△EGF≌Rt△EDF(HL),
∴GF=DF;
(2)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=2DF,
∴CF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x;
在Rt△BCF中,BC2+CF2=BF2,即y2+x2=(3x)2
∴y=2![]() x,
x,
∴![]() ;
;
(3)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=nDF,
∴BF=BG+GF=(n+1)x
在Rt△BCF中,BC2+CF2=BF2,即y2+[(n-1)x]2=[(n+1)x]2
∴y=2x![]() ,
,
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.
(1)用尺规作图的方法分别作出△ABC的角平分线BE和CF, 且BE和CF交于点O.(保留作图痕迹,不要求写出作法);
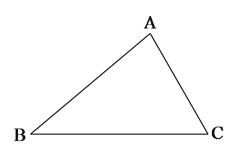
(2)在(1)中,如果∠ABC=40°,,∠ACB=60°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,广州市自2012年以来对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180千瓦时(含180千瓦时)以内的部分,执行基本价格;第二档为用电量在180千瓦时到450千瓦时(含450千瓦时)的部分,实行提高电价;第三档为用电量超出450千瓦时的部分,比第二档的单价每千瓦时提高0.05元. 海珠区的李白同学家今年2月份用电330千瓦时,电费为213元,3月份用电240千瓦时,电费为150元.已知我市的另一位居民杜甫家今年4、5月份的家庭用电量分别为200和 490千瓦时,请你依据题目条件,计算杜甫家4、8月份的电费分别为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com