
分析 (1)根据方程的系数结合根的判别式,即可得出△=(m-1)2+3>0,由此即可证出此方程有两个不相等的实数根;
(2)取m=0,再利用分解因式法解一元二次方程,即可得出方程的解.
解答 (1)证明:△=m2-4($\frac{1}{2}$m-1)=m2-2m+4=(m-1)2+3.
∵(m-1)2+3>0,即△>0,
∵无论m取何值时,(m-1)2≥0,
∴(m-1)2+3>0,即△>0.
∴此方程有两个不相等的实数根.
(2)解:取m=0,此时原方程为x2-1=(x+1)(x-1)=0,
解得:x1=1,x2=-1.
点评 本题考查了根的判别式以及因式分解法解一元二次方程,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根”;(2)熟练掌握一元二次方程的各种解法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度但不超过300度的部分 | 0.65 |
| 超过300度的部分 | 0.9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
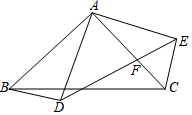 如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形,DE交AC于点F.
如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形,DE交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
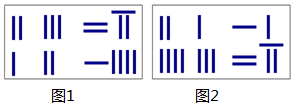 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{2x+3y=27}\\{x+2y=14}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )
《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{2x+3y=27}\\{x+2y=14}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )| A. | $\left\{\begin{array}{l}{2x+y=16}\\{4x+3y=22}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=16}\\{4x+3y=27}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=27}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=22}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com