
【题目】如图1,点O为正方形ABCD 的中心,E为AB 边上一点,F为BC边上一点,△EBF的周长等于 BC 的长.
(1)求∠EOF 的度数.
(2)连接 OA、OC(如图2).求证:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.
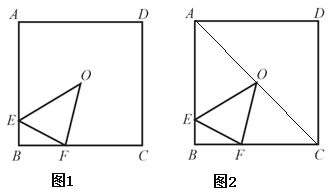
【答案】(1)45°;(2)证明见解析;(3)![]()
【解析】分析:(1)、在BC上取一点G,使得CG=BE,连接OB、OC、OG,然后证明△OBE和△OCG全等,从而得出∠BOE=∠COG,∠BEO=∠CGO,OE=OG,根据三角形的周长得出EF=GF,从而得出△FOE和△GOF全等,得出∠EOF的度数;(2)、连接OA,根据点O为正方形ABCD的中心得出∠OAE=∠FCO=45°,结合∠BOE=∠COG得出∠AEO=∠COF,从而得出三角形相似;(3)、根据相似得出线段比,根据相似比求出AE和CO的关系,CF和AO的关系,从而得出答案.
详解:解:(1)、如图,在BC上取一点G,使得CG=BE,连接OB、OC、OG.
∵点O为正方形ABCD的中心, ∴ OB=OC,∠BOC=90°,∠OBE=∠OCG=45°.
∴△OBE≌△OCG(SAS). ∴∠BOE=∠COG,∠BEO=∠CGO,OE=OG.
∴∠EOG=90°,∵△BEF的周长等于BC的长,
∴ EF=GF. ∴△EOF≌△GOF(SSS).∴∠EOF=∠GOF=45°.
(2)、连接OA.∵ 点O为正方形ABCD的中心, ∴∠OAE=∠FCO=45°.
∵∠BOE=∠COG, ∠AEO=∠BOE+∠OBE=∠BOE+45°,
∠COF=∠COG+∠GOF=∠COG+45°. ∴ ∠AEO=∠COF,且∠OAE=∠FCO.
∴ △AOE∽△CFO.
(3)、∵△AOE∽△CFO,∴![]() =
=![]() =
=![]() .即AE=
.即AE= ![]() ×CO,CF=AO÷
×CO,CF=AO÷![]() .
.
∵OE=![]() OF,∴
OF,∴![]() =
=![]() .∴AE=
.∴AE=![]() CO,CF=
CO,CF=![]() AO. ∴
AO. ∴![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
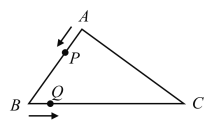
【题目】如图,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发以2个单位长度/秒的速度沿
出发以2个单位长度/秒的速度沿![]() 的方向运动,点
的方向运动,点![]() 从点
从点![]() 沿
沿![]() 的方向与点
的方向与点![]() 同时出发;当点
同时出发;当点![]() 第一次回到
第一次回到![]() 点时,点
点时,点![]() ,
,![]() 同时停止运动;用
同时停止运动;用![]() (秒)表示运动时间.
(秒)表示运动时间.
(1)当![]() 为多少时,
为多少时,![]() 是
是![]() 的中点;
的中点;
(2)若点![]() 的运动速度是
的运动速度是![]() 个单位长度/秒,是否存在
个单位长度/秒,是否存在![]() 的值,使得
的值,使得![]() ;
;
(3)若点![]() 的运动速度是
的运动速度是![]() 个单位长度/秒,当点
个单位长度/秒,当点![]() ,
,![]() 是
是![]() 边上的三等分点时,求
边上的三等分点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
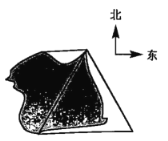
【题目】如图所示,某湖上风景区有两个观望点A,C和两个度假村B、D;度假村D在C正西方向,度假村B在C的南偏东![]() 方向,度假村B到两个观望点的距离都等于2km.
方向,度假村B到两个观望点的距离都等于2km.
(1)在图中标出A、B、C、D的位置,并写出道路CD与CB的夹角.
(2)如果度假村D到C是直公路,长为1km,D到A是环湖路,度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程.求出环湖路的长.
(3)根据题目中的条件,能够判定![]() 吗?若能,请写出判断过程;若不能,请你添加一个条件,判定
吗?若能,请写出判断过程;若不能,请你添加一个条件,判定![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
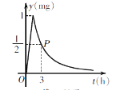
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市移动通讯公司开设了两种通讯业务,A类是固定用户:先缴50元月租费,然后每通话1分钟再付话费0.4元;B类是“神州行”用户:使用者不缴月租费,每通话1分钟付话费0.6元(这里均指市内通话)。如果一个月内通话时间为x分钟,分别设A类和B类两种通讯方式的费用为y![]() 元和y
元和y![]() 元,
元,
(1)写出y![]() 、y
、y![]() 与x之间的函数关系式。
与x之间的函数关系式。
(2)一个月内通话多少分钟,用户选择A类合算?B类呢?
(3)若某人预计使用话费150元,他应选择哪种方式合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com