
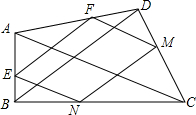
 如图,在四边形ABCD中,∠ABC=90°,点E,F,M,N分别在AB,AD,DC,CB边上,连接EF,EN,NM,FM,若EF∥BD∥NM,$\frac{EN}{AC}$+$\frac{EF}{BD}$=1.
如图,在四边形ABCD中,∠ABC=90°,点E,F,M,N分别在AB,AD,DC,CB边上,连接EF,EN,NM,FM,若EF∥BD∥NM,$\frac{EN}{AC}$+$\frac{EF}{BD}$=1.分析 (1)首先证明$\frac{EN}{AC}$=$\frac{BE}{BA}$,作EN′∥AC交BC于N′,利用同一法证明N与N′重合即可解决问题.
(2)结论:菱形.首先证明四边形MNEF是平行四边形,由S平行四边形MNEF=S-(S△DFM+S△BEN)-(S△AEF+S△CMN)=S-$\frac{E{N}^{2}}{A{C}^{2}}•S$-$\frac{E{F}^{2}}{B{D}^{2}}•S$=$\frac{2EN•EF}{B{D}^{2}}$•S,可知当EF=EN时,EN•EF定值最大,即四边形MNEF的面积最大,此时四边形MNEF是菱形.
解答 (1)证明: ∵EF∥BD,
∵EF∥BD,
∴$\frac{EF}{BD}$=$\frac{AE}{AB}$,
∵$\frac{EN}{AC}$+$\frac{EF}{BD}$=1,
∴$\frac{EN}{AC}$+$\frac{AE}{AB}$=1.
∴$\frac{EN}{AC}$=$\frac{BE}{BA}$,作EN′∥AC交BC于N′,
∴$\frac{BE}{BA}$=$\frac{EN′}{AC}$=$\frac{EN}{AC}$,
∴N与N′重合,
∴EN∥AC,
∴Rt△ABC∽Rt△EBN.
(2)结论:菱形.
理由:∵BD=EF+EN,
∴EF=BD-EN,
∴$\frac{EN}{AC}$+$\frac{BD-EN}{BD}$=1,
∴$\frac{EN}{AC}$=$\frac{EN}{BD}$,
∴AC=BD,
∵EF∥BD,
∴$\frac{FD}{AD}$=$\frac{BE}{AB}$,
∵NE∥AC,
∴$\frac{BE}{AB}$=$\frac{BN}{BC}$,
∵MN∥BD,
∴$\frac{BN}{BC}$=$\frac{DM}{DC}$,
∴$\frac{DF}{DA}$=$\frac{DM}{DC}$,
∴FM∥AC,
∵EF∥MN,
∴四边形MNEF是平行四边形,是四边形ABCD的面积为S,
则有S平行四边形MNEF=S-(S△DFM+S△BEN)-(S△AEF+S△CMN)=S-$\frac{E{N}^{2}}{A{C}^{2}}•S$-$\frac{E{F}^{2}}{B{D}^{2}}•S$=$\frac{2EN•EF}{B{D}^{2}}$•S,
∵EF+EN为定值,
∴当EF=EN时,EN•EF定值最大,即四边形MNEF的面积最大,
此时四边形MNEF是菱形.
点评 本题考查相似三角形的判定和性质、平行线的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,理解两个变量和为定值,相等时积最大是难点,题目比较难.


科目:初中数学 来源: 题型:解答题
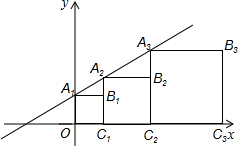 如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.| 坐标 | A1(0,1) | A2(1, 2) | A3( 3, 4) |
| 正方形边长 | A1OC1B1:1 | A2C1C2B2: 2 | A3C2C3B3: 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
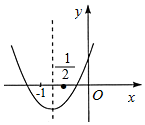 二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c-b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c-b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
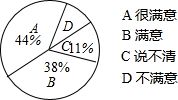 某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有14名.
某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意的有14名.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{7}$ | B. | $1\frac{1}{7}$ | C. | $-\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com