
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2 , 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求x取何值时,花园面积S最大,并求出花园面积S的最大值.
【答案】
(1)解:∵AB=x,则BC=(28-x),
∴x(28-x)=192,
解得:x1=12,x2=16,
答:x的值为12或16
(2)解:∵AB=xm,
∴BC=28-x,
∴S=x(28-x)=-x2+28x=-(x-14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是15m和6m,
∵28-15=13,
∴6≤x≤13,
∴当x=13时,S取到最大值为:S=-(13-14)2+196=195,
答:花园面积S的最大值为195平方米
【解析】(1)根据花园的面积可可列出关于x的方程,解方程可求得x的值;
(2)易得S关于x的函数关系式,根据P的位置可确定x的范围,根据二次函数的性质可求出其最大值.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 向右平移
向右平移![]() 个单位长度得到线段
个单位长度得到线段![]() (点
(点![]() 和点
和点![]() 分别是点
分别是点![]() 和点
和点![]() 的对应点),连接
的对应点),连接![]() 、
、![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.

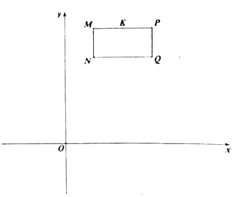
备用图
(1)求点![]() 的坐标;
的坐标;
(2)若长方形![]() 以每秒
以每秒![]() 个单位长度的速度向正下方运动,(点
个单位长度的速度向正下方运动,(点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的对应点),当
的对应点),当![]() 与
与![]() 轴重合时停止运动,连接
轴重合时停止运动,连接![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 妙,请用含
妙,请用含![]() 的式子表示三角形
的式子表示三角形![]() 的面积
的面积![]() (不要求写出
(不要求写出![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() 、
、![]() ,问是否存在某一时刻
,问是否存在某一时刻![]() ,使三角形
,使三角形![]() 的面积等于三角形
的面积等于三角形![]() 的面积?若存在,请求出
的面积?若存在,请求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
如果y′= ![]() ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”
为点(﹣5,﹣6).
(1)①点(2,1)的“关联点”为;②如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数 ![]() 的图象上,那么这个点是(填“点A”或“点B”).
的图象上,那么这个点是(填“点A”或“点B”).
(2)①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”,
那么点M的坐标为;②如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标 .
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标
y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明上星期买进某公司股票7000股,每股27元,下表为本周每日该股票的涨跌情况![]() 单位:元
单位:元![]()
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 |
|
|
|
|
|
|
![]() 这六天中,哪几天的股票是上涨的?哪几天的股票是下跌的?
这六天中,哪几天的股票是上涨的?哪几天的股票是下跌的?
![]() 哪天股票上涨的最多?你能算出这天收盘时每股是多少元吗?
哪天股票上涨的最多?你能算出这天收盘时每股是多少元吗?
![]() 本周六收盘时每股是多少元?
本周六收盘时每股是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.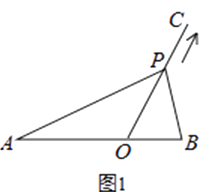
(1)当t= ![]() 秒时,则OP= , S△ABP=;
秒时,则OP= , S△ABP=;
(2)当△ABP是直角三角形时,求t的值;
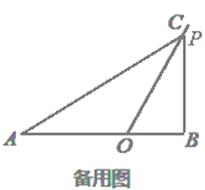
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ·BP=3.为了证明AQ·BP=3,小华同学尝试过O点作OE∥AP交BP于点E.试利用小华同学给我们的启发补全图形并证明AQ·BP=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税;
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税.
试根据上述纳税的计算方法作答:
(1)若王老师获得的稿费为2400元,则应纳税 元,若王老师获得的稿费为4000元,则应纳税 元;
(2)若王老师获稿费后纳税420元,求这笔稿费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机动车出发前油箱中有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
(1)机动车行驶了 小时后加油,加油 升;
(2)加油后油箱中的油最多可行驶多少小时?
(3)加油前油箱余油量Q与行驶时间t的函数关系式是 ;
(4)如果加油站距目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com