
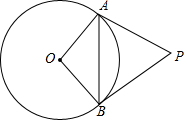
 如图,PA,PB是⊙O的两条切线,A,B是切点,连接AB,已知AB=4.8,OA=3,那么PB的长度为4.
如图,PA,PB是⊙O的两条切线,A,B是切点,连接AB,已知AB=4.8,OA=3,那么PB的长度为4. 分析 连接OP,交AB于点C,利用垂径定理求得BC的长,然后利用勾股定理求得OC的长,证明△OPB∽△OBC,根据相似三角形的对应边的比相等求解.
解答 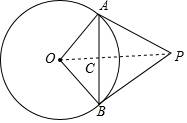 解:连接OP,交AB于点C.
解:连接OP,交AB于点C.
∵PA和PB是⊙O的两条切线,
∴PA=PB,且PO平分∠APB,
∴OP⊥AB,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×4.8=2.4.
∴在直角△OBC中,OC=$\sqrt{O{B}^{2}-B{C}^{2}}$=$\sqrt{{3}^{2}-2.{4}^{2}}$=1.8,
∵PB是⊙O的两条切线,
∴OB⊥PB,
∴△OPB∽△OBC,
∴$\frac{PB}{BC}$=$\frac{OB}{OC}$,即$\frac{PB}{2.4}$=$\frac{3}{1.8}$,
∴PB=4.
故答案是:4.
点评 本题考查了切线长定理以及垂径定理和相似三角形的判定与性质,正确证明△OPB∽△OBC是关键.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:选择题
| A. | 把圆n等分,顺次连接各分点得到的多边形是圆的内接正n边形 | |
| B. | 把圆n等分,依次过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形 | |
| C. | 各边相等.并且各角也相等的多边形是正多边形 | |
| D. | 用量角器等分圆是一种简单而常用的方法 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
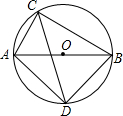 如图,AB为⊙O的直径,AC为⊙O的弦,AB=6,AC=2,∠ACB的平分线交⊙O于点D.
如图,AB为⊙O的直径,AC为⊙O的弦,AB=6,AC=2,∠ACB的平分线交⊙O于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:填空题
体育老师对甲、乙两名同学分别进行了8次跳高测试,经计算这两名同学成绩的平均数相同,甲同学的方差是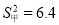 ,乙同学的方差是
,乙同学的方差是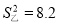 ,那么这两名同学跳高成绩比较稳定的是_____同学.
,那么这两名同学跳高成绩比较稳定的是_____同学.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com