
【题目】为了丰富课外活动,某校将购买一些乒乓球拍和乒乓球,某商场销售一种乒乓球拍和乒乓球,乒乓球拍每副定价80元,乒乓球每盒定价20元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副乒乓球拍送一盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的90%付款.
某校要到该商场购买乒乓球拍20副,乒乓球![]() 盒(
盒(![]() >20且为整数).
>20且为整数).
(1)若按方案一购买,需付款 元(用含![]() 的整式表示,要化简); 若按方案二购买,需付款 元(用含
的整式表示,要化简); 若按方案二购买,需付款 元(用含![]() 的整式表示,要化简).
的整式表示,要化简).
(2)若![]() 30,通过计算说明此时按哪种方案购买较为合算?
30,通过计算说明此时按哪种方案购买较为合算?
(3)当![]() 30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
【答案】(1)方案一费用:20x+1200 ;方案二费用:18x+1440;(2)按方案一购买较合算;;(3)先按方案一购买20副乒乓球拍获赠送20盒乒乓球, 再按方案二购买10盒乒乓球.
【解析】
(1)方案一费用:20副乒乓球拍子费用+(x-20)盒乒乓球费用;方案二费用:(20副乒乓球拍子费用+x盒乒乓球费用)×0.9,把相关数值代入求解即可;
(2)把x=30代入(1)得到的式子进行计算,然后比较结果即可;
(3)根据题意得出方案一购买乒乓球拍子,方案二购买乒乓球,然后再进行计算即可.
(1).方案一费用:20x+1200
方案二费用:18x+1440
(2)当x=30时,方案一:20×30+1200=1800(元)
方案二:18×30+1440=1980(元)
所以,按方案一购买较合算.
(3)先按方案一购买20副乒乓球拍获赠送20盒乒乓球,再按方案二购买10盒乒乓球.则20×80+20×10×90%=1780(元)


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是由一些大小相同的小正方体组合成的简单几何体,并放在墙角.(注:图3、图4、图5每一个小方格的边长为1cm)
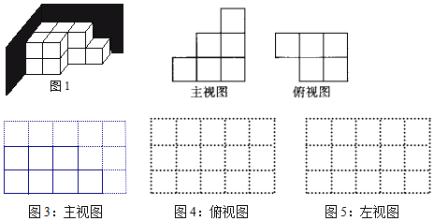
(1)该几何体主视图如图3所示,请在图4方格纸中画出它的俯视图;
(2)若将其露在外面的表面涂一层漆,则其涂漆面积为 cm2.(正方体的棱长为1cm)
(3)用一些小立方块搭一个几何体,使它的主视图和俯视图如图所示,它最少需要多少个小立方块?最多需要多少个小立方块?并在图5方格纸中画出需要最多小立方块的几何体的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
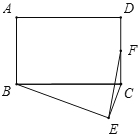
【题目】如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A. 8B. 9C. 10D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 、
、![]() 两个点对应的数分别是
两个点对应的数分别是![]() 、
、![]() ,且满足
,且满足![]() ;
;
![]()
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是数轴上
是数轴上![]() 、
、![]() 之间的一个点,使得
之间的一个点,使得![]() ,求出点
,求出点![]() 所对应的数;
所对应的数;
(3)点![]() ,点
,点![]() 为数轴上的两个动点,点
为数轴上的两个动点,点![]() 从
从![]() 点以3个单位长度每秒的速度向右运动,点
点以3个单位长度每秒的速度向右运动,点![]() 同时从
同时从![]() 点以2个单位长度每秒的速度向左运动,设运动时间为
点以2个单位长度每秒的速度向左运动,设运动时间为![]() 秒,若
秒,若![]() ,求时间
,求时间![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会4×100米是最精彩的比赛项目,下表是七年级1班与2班在比赛时各运动员的接棒时间(假设每名运动员跑步速度不变,交接棒时间忽路不计,每名运动员都恰好跑100m,两个班级均用了55秒的时间达到终点(单位:秒):
班级 | 第二棒接棒时间 | 第三棒接棒时间 | 第四棒接棒时间 |
1班 | 12 | 28 | 40 |
2班 | 13 | 25 | 41 |
(1)两个班级共八名学生中跑的最慢的学生跑完100米用的时间是 秒;
(2)当2班第二棒运动员接棒时,1班运动员领先 米;
(3)求从出发开始计时,多长时间两队第一次并列?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了保护和改善生态环境,决定从2014年起进行“退耕还林”,把易造成水土流失的坡耕地变为林地,并出台了一项激励措施:在“退耕还林”的过程中,每一年新增林地面积达到10亩的农户,当年都可得到生活补贴1500元,且每超出一亩,政府还给予每亩a元的奖励.另外,经“退耕还林”后的林地从下一年起,平均每亩每年可有110元的种树收入.下表是某农户在头两年通过“退耕还林”每年获得的总收入(年总收入=生活补贴费+政府奖励费+种树收入)情况:
年份 | 新增林地亩数 | 年总收入 |
2014 | 20亩 | 2400 |
2015 | 26亩 | 4300元 |
(1)试根据以上提供的资料求a的值;
(2)如果该农户计划在2016年总收入达到10000元,则该农户在2016年应新增林地约多少亩?(结果保留整数)
(3)从2015年起,如果该农户每年新增林地的亩数均能比前一年按相同的增长率增长,那么该农户在2017年新增林地多少亩(结果保留两位小数)?2017年该农户通过“退耕还林”获得的年总收入将达到多少元(结果保留一位小数)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示数a,点B表示数b,点C表示数c.b是最小的正整数,且a、b满足|a+2|+(c﹣7)2=0
(1)填空:a= ,b= .
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与C之间的距离表示为BC.则BC= .(用含t的代数式表示)
(3)请问:|2AB﹣3BC|的值是否随着时间t的变化而改变?若改变,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com