Question

16．如图，已知二次函数y=-$\frac{1}{4}$x²+$\frac{3}{2}$x+4的图象与y轴交于点A，与x轴交于B、C两点，其对称轴与x轴交于点D，连接AC．

（1）点A的坐标为（0，4），点C的坐标为（8，0）；
（2）线段AC上是否存在点E，使得△EDC为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；
（3）点P为x轴上方的抛物线上的一个动点，连接PA、PC，若所得△PAC的面积为S，则S取何值时，相应的点P有且只有两个，并求出此时点P的坐标．

Answer 1

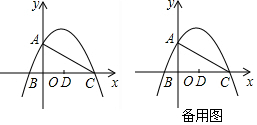
分析 （1）抛物线的解析式中，令x=0即得二次函数与y轴交点A的纵坐标，令y=0即得二次函数与x轴交点的横坐标．
（2）根据A、C的坐标，易求得直线AC的解析式，由于等腰△EDC的腰和底不确定，因此要分成三种情况讨论：
①CD=DE，由于OD=3，OA=4，那么DA=DC=5，此时A点符合E点的要求，即此时A、E重合；
②CE=DE，根据等腰三角形三线合一的性质知：E点横坐标为点D的横坐标加上CD的一半，然后将其代入直线AC的解析式中，即可得到点E的坐标；
③CD=CE，此时CE=5，过E作EG⊥x轴于G，已求得CE、CA的长，即可通过相似三角形（△CEG∽△CAO）所得比例线段求得EG、CG的长，从而得到点E的坐标．
（3）过P作x轴的垂线，交AC于Q，交x轴于H；设出点P的横坐标（设为m），根据抛物线和直线AC的解析式，即可表示出P、Q的纵坐标，从而可得到PQ的长，然后分两种情况进行讨论：
①P点在第一象限时，即0＜m＜8时，可根据PQ的长以及A、C的坐标，分别表示出△APQ、△CPQ的面积，它们的面积和即为△APC的面积，由此可得到S的表达式，通过配方即可得到S的取值范围；
②当P在第二象限时，即-2＜m＜0时，同①可求得△APQ、△CPQ的面积，此时它们的面积差为△APC的面积，同理可求得S的取值范围；根据两个S的取值范围，即可判断出所求的结论．

解答 解：（1）在二次函数中，令x=0得y=4，
∴点A的坐标为（0，4），
令y=0得，-$\frac{1}{4}$x²+$\frac{3}{2}$x+4=0
即：x²-6x-16=0，
∴x=-2和x=8，
∴点B的坐标为（-2，0），点C的坐标为（8，0）．
故答案为：（0，4）；（8，0）．
（2）∵点D是二次函数y=-$\frac{1}{4}$x²+$\frac{3}{2}$x+4的对称轴与x轴的交点，
∴D（3，0），CD=5，
设直线AC对应的函数关系式为y=kx+b，则：$\left\{\begin{array}{l}{b=4}\\{8k+b=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$；
∴y=-$\frac{1}{2}$x+4；
①当DE=DC时，
∵OA=4，OD=3，
∴DA=5，
∴E₁（0，4）；
②如图1，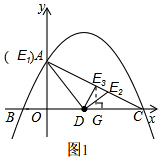

过E点作EG⊥x轴于G点，
当DE=EC时，由DG=$\frac{8-3}{2}$=$\frac{5}{2}$，
把x=OD+DG=3+$\frac{5}{2}$=$\frac{11}{2}$代入到y=-$\frac{1}{2}$x+4，求出y=$\frac{5}{4}$，
可得E₂（$\frac{11}{2}$，$\frac{5}{4}$）；
③当DC=EC时，如图，过点E作EG⊥CD，
则△CEG∽△CAO，
∴$\frac{EG}{OA}=\frac{CG}{OC}=\frac{CE}{AC}$，又OA=4，OC=8，则AC=4$\sqrt{5}$，DC=EC=5，
∴EG=$\sqrt{5}$，CG=2$\sqrt{5}$，
∴E₃（8-2$\sqrt{5}$，$\sqrt{5}$）；
综上所述，符合条件的E点共有三个：E₁（0，4）、E₂（$\frac{11}{2}$，$\frac{5}{4}$）、E₃（8-2$\sqrt{5}$，$\sqrt{5}$）．

（3）如图2，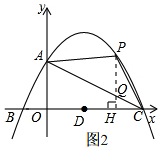

过P作PH⊥OC，垂足为H，交直线AC于点Q；
设P（m，-$\frac{1}{4}$m²+$\frac{3}{2}$m+4），则Q（m，-$\frac{1}{2}$m+4）．
①当0＜m＜8时，
PQ=（-$\frac{1}{4}$m²+$\frac{3}{2}$m+4）-（-$\frac{1}{2}$m+4）=-$\frac{1}{4}$m²+2m，
S=S_△APQ+S_△CPQ=$\frac{1}{2}$×8×（-$\frac{1}{4}$m²+2m）=-（m-4）²+16，
∴0＜S≤16；
②当-2≤m＜0时，
PQ=（-$\frac{1}{2}$m+4）-（-$\frac{1}{4}$m²+$\frac{3}{2}$m+4）=$\frac{1}{4}$m²-2m，
S=S_△CPQ-S_△APQ=$\frac{1}{2}$×8×（$\frac{1}{4}$m²-2m）=（m-4）²-16，
∴0＜S＜20；
∴当0＜S＜16时，0＜m＜8中有m两个值，-2＜m＜0中m有一个值，此时有三个；
当16＜S＜20时，-2＜m＜0中m只有一个值；
当S=16时，m=4或m=4-4$\sqrt{2}$或m=4+4$\sqrt{2}$（舍），
∴S=16时，相应的点P有且仅有两个，
当m=4时，S=16，
∴y=-$\frac{1}{4}$m²+$\frac{3}{2}$m+4=6，
∴P（4，6），
当m=4-4$\sqrt{2}$时，y=-$\frac{1}{4}$m²+$\frac{3}{2}$m+4=2$\sqrt{2}$-2，
∴P（4-2$\sqrt{2}$，2$\sqrt{2}$-2），
即：P（4，6）或（4-2$\sqrt{2}$，2$\sqrt{2}$-2）．

点评 此题是二次函数综合题，主要考查了二次函数图象与坐标轴交点坐标的求法、等腰三角形的构成条件、图形面积的求法等知识，（3）题的解题过程并不复杂，关键在于理解题意．