
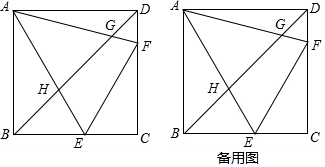
 如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.
如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.分析 (1)易证∠BAG=∠AHD,∠ABD=∠ADB=45°,即可证明△ABG∽△HDA,可得$\frac{AB}{DH}=\frac{BG}{DA}$,即可得出结论;
(2)首先连接AC,由正方形ABCD,∠EAF=45゜,易证得∠ACE=∠ADN=∠CAD=45°,AC=$\sqrt{2}$AD,继而可得∠EAC=∠NAD,则可证得△EAC∽△NAD,然后由相似三角形的对应边成比例,证得结论;
(3)根据两边的比相等,且夹角相等证明△GAH∽△EAF,得$\frac{EF}{GH}=\sqrt{2}$,所以EF=$\sqrt{2}$GH.
解答 证明:(1)∵四边形ABCD为正方形
∴∠ABD=∠ADB=45°,AB=AD,
∵∠EAF=45°
∴∠BAG=45°+∠BAH,∠AHD=45°+∠BAH,
∴∠BAG=∠AHD,
又∵∠ABD=∠ADB=45°,
∴△ABG∽△HDA,
∴$\frac{AB}{DH}=\frac{BG}{DA}$,
∴BG•DH=AB•AD=AD2;
(2)如图,连接AC,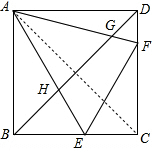
∵四边形ABCD是正方形
∴∠ACE=∠ADB=∠CAD=45°,
∴AC=$\sqrt{2}$AD,
∵∠EAF=45°,
∴∠EAF=∠CAD,
∴∠EAF-∠CAF=∠CAD-∠CAF,
∴∠EAC=∠GAD,
∴△EAC∽△GAD,
∴$\frac{CE}{DG}=\frac{AC}{AD}=\sqrt{2}$,
∴CE=$\sqrt{2}$DG;
(3)由(2)得:△EAC∽△GAD,
∴$\frac{AE}{AG}=\frac{AC}{AD}=\sqrt{2}$,
同理得:△AFC∽△AHB,
∴$\frac{AF}{AH}=\frac{AC}{AB}=\sqrt{2}$,
∴$\frac{AE}{AG}=\frac{AF}{AH}=\sqrt{2}$,
∴$\frac{AE}{AG}=\frac{AF}{AH}$,
∵∠GAH=∠EAF,
∴△GAH∽△EAF,
∴$\frac{EF}{GH}=\sqrt{2}$,
∴EF=$\sqrt{2}$GH.
点评 本题考查了相似三角形的判定和性质,常运用两角相等判定两三角形相似,并熟练掌握相似三角形对应边成比例的性质,第三问有难度,证明△GAH∽△EAF是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
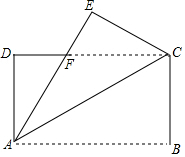 如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.
如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)2017 | B. | (-3)0 | C. | $\sqrt{9}$ | D. | ($\frac{1}{2}$)-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
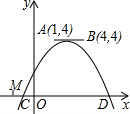
 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
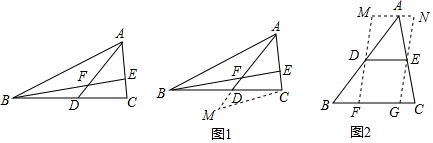
 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{20}{3}$ | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
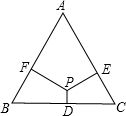
 如图,点A,B的坐标分别为(1,4)和(4,4),将抛物线y=a(x-m)2+n平移并保持顶点在线段AB上,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则当点D的横坐标达到最大值时抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4.
如图,点A,B的坐标分别为(1,4)和(4,4),将抛物线y=a(x-m)2+n平移并保持顶点在线段AB上,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则当点D的横坐标达到最大值时抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com