
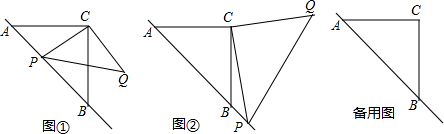
分析 (1)①在Rt△ABC中,可求得AB,由PB=AB-PA可求得PB,过C作CD⊥AB于点D,则可求得CD=AD=DB,可求得PD的长,在Rt△PCD中可求得PC的长;②把AP2和PB2都用PC和CD表示出来,结合Rt△PCD中,可找到PC和PD和CD的关系,从而可找到PA2,PB2,PQ2三者之间的数量关系;
(2)过C作CD⊥AB于点D,由(1)中②的方法,可证得结论;
(3)分点P在线段AB上和线段BA的延长线上,分别利用$\frac{PA}{PB}$=$\frac{1}{3}$可找到PA和CD的关系,从而可找到PD和CD的关系,在Rt△CPD和Rt△ACD中,利用勾股定理可分别找到PC、AC和CD的关系,从而可求得$\frac{PC}{AC}$的值.
解答 解:
(1)①∵△ABC是等腰直角三角形,AC=1+$\sqrt{3}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2A{C}^{2}}$=$\sqrt{2}$+$\sqrt{6}$,
∵PA=$\sqrt{2}$,
∴PB=AB-PA=$\sqrt{6}$,
如图1,过C作CD⊥AB于点D,则AD=CD=$\frac{1}{2}$AB=$\frac{\sqrt{2}+\sqrt{6}}{2}$,
∴PD=AD-PA=$\frac{\sqrt{6}-\sqrt{2}}{2}$,
在Rt△PCD中,PC=$\sqrt{P{D}^{2}+C{D}^{2}}$=2,
故答案为:$\sqrt{6}$;2;
②PA2+PB2=PQ2,
证明如下:
如图1,∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB,
∵PA2=(AD-PD)2=(CD-PD)2=CD2-2CD•PD+PD2,PB2=(BD+PD)2=(CD+PD)2=CD2-2CD•PD+PD2,
∴PA2+PB2=2CD2+2PD2=2(CD2+PD2),
在Rt△PCD中,由勾股定理可得PC2=CD2+PD2,
∴PA2+PB2=2PC2,
∵△CPQ为等腰直角三角形,且∠PCQ=90°,
∴2PC2=PQ2,
∴PA2+PB2=PQ2,
故答案为:PA2+PB2=PQ2;
(2)证明:
如图2,过C作CD⊥AB于点D,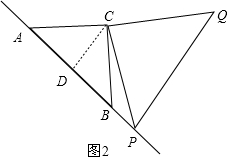
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB,
∵PA2=(AD+PD)2=(CD+PD)2=CD2-2CD•PD+PD2,PB2=(DP-BD)2=(PD-CD)2=CD2-2CD•PD+PD2,
∴PA2+PB2=2CD2+2PD2=2(CD2+PD2),
在Rt△PCD中,由勾股定理可得PC2=CD2+PD2,
∴PA2+PB2=2PC2,
∵△CPQ为等腰直角三角形,且∠PCQ=90°,
∴2PC2=PQ2,
∴PA2+PB2=PQ2;
(3)过点C作CD⊥AB于点D,
∵$\frac{PA}{PB}$=$\frac{1}{3}$,
∴点P只能在线段AB上或在线段BA的延长线上,
①如图3,当点P在线段AB上时,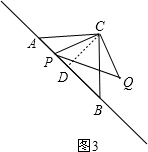
∵$\frac{PA}{PB}$=$\frac{1}{3}$,
∴PA=$\frac{1}{4}$AB=$\frac{1}{2}$CD=PD,
在Rt△CPD中,由勾股定理可得CP=$\sqrt{C{D}^{2}+P{D}^{2}}$=$\sqrt{C{D}^{2}+(\frac{1}{2}CD)^{2}}$=$\frac{\sqrt{5}}{2}$CD,
在Rt△ACD中,由勾股定理可得AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{2C{D}^{2}}$=$\sqrt{2}$CD,
∴$\frac{PC}{AC}$=$\frac{\frac{\sqrt{5}}{2}CD}{\sqrt{2}CD}$=$\frac{\sqrt{10}}{4}$;
②如图4,当点P在线段BA的延长上时,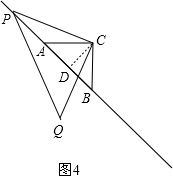
∵$\frac{PA}{PB}$=$\frac{1}{3}$,
∴PA=$\frac{1}{2}$AB=CD,
在Rt△CPD中,由勾股定理可得CP=$\sqrt{C{D}^{2}+P{D}^{2}}$=$\sqrt{{CD}^{2}+(2CD)^{2}}$=$\sqrt{5}$CD,
在Rt△ACD中,由勾股定理可得AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{2C{D}^{2}}$=$\sqrt{2}$CD,
∴$\frac{PC}{AC}$=$\frac{\sqrt{5}CD}{\sqrt{2}CD}$=$\frac{\sqrt{10}}{2}$;
综上可知$\frac{PC}{AC}$的值为$\frac{\sqrt{10}}{4}$或$\frac{\sqrt{10}}{2}$.
点评 本题主要考查等腰直角三角形的性质和勾股定理的应用,并涉及分类讨论思想.在(2)中注意分别用CD和PD表示出PA和PB是解题的关键,在(3)中确定出P点的位置,再结合条件找到PC、AC与CD的关系是解题的关键.本题涉及内容不多,但综合性很强,难度较大.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
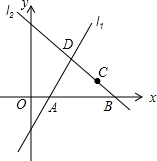 如图,直线l1的解析式为y=2x-2,且l1与x轴交于点A,直线l2经过B(4,0),C(3,1),直线l1、l2交于点D.
如图,直线l1的解析式为y=2x-2,且l1与x轴交于点A,直线l2经过B(4,0),C(3,1),直线l1、l2交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+$\sqrt{3}$=2$\sqrt{3}$ | B. | $\sqrt{8}÷\sqrt{2}$=2 | C. | (-2a2)3=-6a6 | D. | (a+1)2=a2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2)-2=4 | B. | $\sqrt{{{(-2)}^2}}=-2$ | C. | 46÷(-2)6=64 | D. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
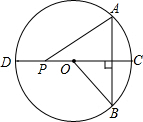 如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是60°<β<75°.
如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是60°<β<75°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com