
【题目】如图,已知![]() ,
,![]() 、
、![]() 的交点为
的交点为![]() ,现作如下操作:
,现作如下操作:
第一次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第二次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第三次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
…
第![]() 次操作,分别作
次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() .
.
若![]() 度,那
度,那![]() 等于__________度.
等于__________度.


【答案】![]()
【解析】
先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;根据∠ABE和∠DCE的平分线交点为E1,则可得出∠CE1B=∠ABE1+∠DCE1![]() ∠ABE
∠ABE![]() ∠DCE
∠DCE![]() ∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2
∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2![]() ∠ABE1
∠ABE1![]() ∠DCE1
∠DCE1![]() ∠CE1B
∠CE1B![]() ∠BEC;根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C
∠BEC;根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C![]() ∠BEC;…据此得到规律∠En
∠BEC;…据此得到规律∠En![]() ∠BEC,最后求得∠BEC的度数.
∠BEC,最后求得∠BEC的度数.
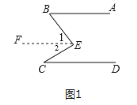
如图1,过E作EF∥AB.
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2.
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
如图2.
∵∠ABE和∠DCE的平分线交点为E1,
∴∠CE1B=∠ABE1+∠DCE1![]() ∠ABE
∠ABE![]() ∠DCE
∠DCE![]() ∠BEC.
∠BEC.
∵∠ABE1和∠DCE1的平分线交点为E2,
∴∠BE2C=∠ABE2+∠DCE2![]() ∠ABE1
∠ABE1![]() ∠DCE1
∠DCE1![]() ∠CE1B
∠CE1B![]() ∠BEC;
∠BEC;
∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3![]() ∠ABE2
∠ABE2![]() ∠DCE2
∠DCE2![]() ∠CE2B
∠CE2B![]() ∠BEC;
∠BEC;
…
以此类推,∠En![]() ∠BEC,
∠BEC,
∴当∠En=1度时,∠BEC等于2n度.
故答案为:2n.



科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁一起研究一道数学题,如图,已知 EF⊥AB,CD⊥AB,甲说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.”乙说:“如果还知道∠AGD=∠ACB,则能得到∠CDG=∠BFE.”丙说:“∠AGD 一定大于∠BFE.”丁说:“如果连接 GF,则 GF∥AB.”他们四人中,正确的是( )
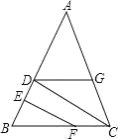
A.0 个B.1 个C.2 个D.3 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,若四边形ABCD为“可分四边形”,∠DAB为“可分角”,且∠DCB=∠DAB,则∠DAB=°.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试.某校对初三学生进行了模拟训练.物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定.小张同学对物理的①、②和化学的b、c实验准备得较好,请用树形图或列表法求他两科都抽到准备得较好的实验题目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF,若∠ABE=25°,则∠EFC'的度数为( )
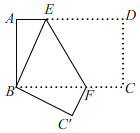
A.122.5°B.130°C.135°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
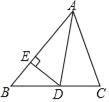
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
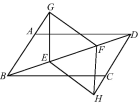
【题目】如图,在ABCD中,E,F是对角线BD上的两点,BE=DF,点G,H分别在BA和DC的延长线上,且AG=CH,连接GE,EH,HF,FG.
(1)求证:四边形GEHF是平行四边形;
(2)若点G,H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=![]() ,则下列等式中对于任意实数 a、b、c 都成立的是( )
,则下列等式中对于任意实数 a、b、c 都成立的是( )
①a+(b*c)=(a+b)*(a+c) ②a*(b+c)=(a+b)*c
③a*(b+c)=(a*b)+(a*c) ④(a*b)+c= ![]() +(b*2c)
+(b*2c)
A. ①②③ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com