

分析 根据全等三角形对应角相等,可以证明AC∥DE∥HF,再根据全等三角形对应边相等BC=CE=EF,然后利用平行线分线段成比例定理求出HF=3PC,KE=2PC,所以PC=DK,设△DQK的边DK为x,DK边上的高为h,表示出△DQK的面积,再根据边的关系和三角形的面积公式即可求出三部分阴影部分的面积.
解答 解:∵△ABC≌△DCE≌△HEF,
∴∠ACB=∠DEC=∠HFE,BC=CE=EF,
∴AC∥DE∥HF,
∴$\frac{PC}{KE}=\frac{BC}{BE}$=$\frac{1}{2}$,$\frac{PC}{HF}$=$\frac{BC}{BF}$=$\frac{1}{3}$,
∴KE=2PC,HF=3PC,
又∵DK=DE-KE=3PC-2PC=PC,
∴△DQK≌△CQP(相似比为1)
设△DQK的边DK为x,DK边上的高为h,
则$\frac{1}{2}$xh=1,整理得xh=2,
S△BPC=$\frac{1}{2}$x•2h=xh=2,
S四边形CEKQ=$\frac{1}{2}$×3x•2h-2=3xh-2=3×2-1=6-1=5,
S△EFH=$\frac{1}{2}$×3x•2h=3xh=6,
∴三个阴影部分面积的和为:2+5+6=13.
故答案为13.
点评 本题主要利用全等三角形的性质,找出阴影部分的图形边的关系和三角形的面积公式的解题的关键.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
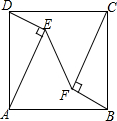 如图,在正方形ABCD中,分别以AD,BC为斜边作Rt△ADE和Rt△CBF,且Rt△ADE≌Rt△CBF,连结EF,若S正方形ABCD=20,S△ADE=3,则EF=4.
如图,在正方形ABCD中,分别以AD,BC为斜边作Rt△ADE和Rt△CBF,且Rt△ADE≌Rt△CBF,连结EF,若S正方形ABCD=20,S△ADE=3,则EF=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com