
����Ŀ���ס������̳����ж�������ijһ��Ʒ��
��1�����̳�������Ʒ���25%����ۼ�Ϊ1.25Ԫ�������Ʒ�ڼ��̳���ԭ��Ϊ�� ��Ԫ��
��2�����̳����������ַ���������������Ʒ���20%������������Ʒ���1Ԫ��ij�˿ͷ��������̳���60ԪǮ�������Ʒ������������ļ����ǰ���������ļ�����2����10���������Ʒ�����̳���ԭ���Ƕ��٣�
��3���ס������̳��Ѹ���Ʒ����ԭ�۽��������μ۸���������̳�����һ����۵İٷ�����a���ڶ�����۵İٷ�����b�����̳���������۵İٷ��ʶ���![]() ��a��0��b��0��a��b�������ʼס������̳����ĸ��̳�����۽϶ࣿ��˵�����ɣ�
��a��0��b��0��a��b�������ʼס������̳����ĸ��̳�����۽϶ࣿ��˵�����ɣ�
���𰸡���1��1Ԫ����2��1Ԫ;��3�����̳�������ۺ�۸�϶�,���ɼ�����.
��������������(1)�����������ʽ:�ۼ�-����=����,ֱ����ռ���;
(2)�����Ʒ�����̳���ԭ��ΪxԪ,������ۺ�, ��60ԪǮ����������ļ����ǰ���������ļ�����2����10���������з������.
(3)�ֱ�����ס������̳���ۺ�Ĵ���ʽ,�Ƚϴ�С�������.
���������
��1��1.25�£�1+25%��=1��Ԫ��
��2�������Ʒ�����̳���ԭ��ΪxԪ����
![]() ��
��
�����飺x=1���㷽�̣�����ʵ�ʣ�
�𣺸���Ʒ�����̳���ԭ��Ϊ1Ԫ��
��3������ԭ�۾�Ϊ1Ԫ����
���̳�������ۺ�ļ۸�Ϊ����1+a����1+b��=1+a+b+ab��
���̳�������ۺ�ļ۸�Ϊ�� ![]() ��
��
��![]()
�����̳�������ۺ�۸�϶࣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܰ�һ�������ηֳ�����ֱ�������ε��������εģ� ��
A.��
B.��ƽ����
C.����
D.���ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A������Ϊ(3��4)����A����x��ԳƵĵ�������ǣ� ��
A. ����3��4�� B. ��3����4�� C. ����3����4�� D. ��4��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�β�����Գ�ͼ�ε��ǣ� ��
A.ƽ���ı���
B.����������
C.������
D.Բ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֤���عˡ�֤������������λ�߶�����
��֪����ͼ1��DE�ǡ�ABC����λ�ߣ�
��֤���� ����
֤�������Ӹ����ߣ���ͼ1���ڡ�ABC�У��ӳ�DE ��D��E�ֱ���AB��AC���е㣩����F��ʹ��EF=DE������CF��
��������֤�����̣�

��2������������
��ͼ2����������ABCD�У�EΪAD���е㣬G��F�ֱ�ΪAB��CD���ϵĵ㣬��AG=2��DF=3����GEF=90�㣬��GF�ij���
��3������չ�о���
��ͼ3�����ı���ABCD�У���A=105�㣬��D=120�㣬EΪAD���е㣬G��F�ֱ�ΪAB��CD���ϵĵ㣬��AG=![]() ��DF=2����GEF=90�㣬��GF�ij���
��DF=2����GEF=90�㣬��GF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪,ƽ���ı���ABCD���ܳ�Ϊ20cm����AD-AB=2cm����AD=_________cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
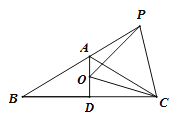
����Ŀ��������ABC�У�AB=AC����BAC=120�㣬AD��BC��D����P��BA�ӳ�����һ�㣬��O���߶�AD��һ�㣬OP=OC�����½��ۣ��١�APO=��DCO; �ڡ�APO+��DCO=30�㣻�ۡ�OPCΪ�ȱ������Σ���AC=AD+AP����![]() . ������ȷ���У� ��
. ������ȷ���У� ��
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com