
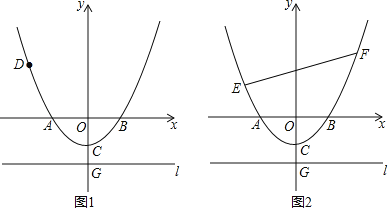
【题目】已知如图1,在以O为原点的平面直角坐标系中,抛物线y=![]() x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.
x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.
(1)求抛物线对应的二次函数的解析式;
(2)若D(﹣4,m)为抛物线y=![]() x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.
x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.
(3)如图2,若E(﹣4,m)为上述抛物线上一点,在抛物线上是否存在点F,使得△BEF是直角三角形,若存在求出点F的坐标,若不存在说明理由.
【答案】(1)y=![]() x2﹣1;(2)t=﹣2;(3)存在点F,使得△BEF是直角三角形,点F的坐标为(6,8).
x2﹣1;(2)t=﹣2;(3)存在点F,使得△BEF是直角三角形,点F的坐标为(6,8).
【解析】
(1)根据点C坐标,可得c=﹣1,然后根据AO=2CO,可得出点A坐标,将点A坐标代入求出b值,即可得出函数解析式;
(2)根据抛物线的解析式求得D的坐标为(﹣4,3),即可求得OD=5,结合D的纵坐标3,即可求得t=﹣2.
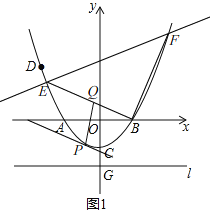
(3)分两种情况讨论:当B点为直角顶点时,则BF⊥BE,根据直线BE的解析式求得直线BF的解析式,然后和抛物线解析式联立方程,求得交点坐标即可;当F点为直角顶点时,求得到直线BE上距离为最大值的点P的坐标,然后求得线段BE的中点Q到P点的距离,和BE的一半比较即可判断以BE为直径的圆与抛物线无交点,故此种情况不存在,综上求得F点的坐标.
(1)∵C(0,﹣1),
∴y=![]() x2+bx﹣1,
x2+bx﹣1,
又∵AO=2OC,
∴点A坐标为(﹣2,0),
代入得:1﹣2b﹣1=0,
解得:b=0,
∴解析式为:y=![]() x2﹣1;
x2﹣1;
(2)∵D(﹣4,m)为抛物线y=![]() x2﹣1上一定点,
x2﹣1上一定点,
∴m=![]() ×16﹣1=3,
×16﹣1=3,
∴D(﹣4,3),
∴OD=![]() =5,
=5,
∴d=5,
∴t=﹣(5﹣3)=﹣2;
(3)点E(﹣4,m)在抛物线y=![]() x2﹣1的上,
x2﹣1的上,
∴m=3,
∴E(﹣4,3),
∵B(2,0),
∴直线BE为y=﹣![]() x+1,
x+1,
如图1,当B点为直角顶点时,则BF⊥BE,
∴直线BF的斜率为2,
设直线BF的解析式为y=2x+n,
把B(2,0)代入得2×2+n=0,
∴n=﹣4,
∴直线BF的解析式为y=2x﹣4,
解 得
得![]() 或
或![]() ,
,
∴F(6,8);
当F点为直角顶点时,
设BE的平行线y=﹣![]() x+b与抛物线有且只有一个交点P,
x+b与抛物线有且只有一个交点P,
∴﹣![]() x+b=
x+b=![]() x2﹣1,
x2﹣1,
整理得x2+2x﹣4b﹣4=0,
∴![]() =4+4(4b+4)=0,
=4+4(4b+4)=0,
解得b=﹣![]() ,
,
∴平行线为y=﹣![]() ﹣
﹣![]() ,
,
∴x2+2x+1=0,
解得x=﹣1,
∴y=﹣![]() ,
,
∴平行线与抛物线的交点P为(﹣1,﹣![]() ),
),
∵B(2,0),E(﹣4,3),
∴BE=![]() ,
,
∴BE的中点Q为(﹣1,![]() ),
),
∴QP=![]() +
+![]() =
=![]() <
<![]() =BE,
=BE,
∴此种情况不存在,
故在抛物线上存在点F,使得△BEF是直角三角形,点F的坐标为(6,8).


科目:初中数学 来源: 题型:
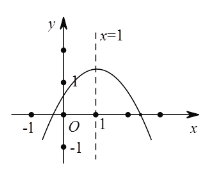
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③a-b+c>0;④当x≠1时,a+b>ax2+bx:⑤4ac<b2.其中正确的有____________(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+6x+c交x轴于A、B两点,交y轴于点C.直线y=x﹣5经过点B、C.
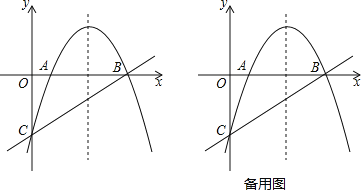
(1)求抛物线的解析式;
(2)过点A作AM⊥BC于点M,过抛物线上一动点P(不与点B、C重合),作直线AM的平行线交直线BC于点Q,若以点A、M、P、Q为顶点的四边形是平行四边形,求点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当x≤3时,函数y=x2﹣2x﹣3的图象记为G,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M,若直线y=x+b与图象M有且只有两个公共点,则b的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD的对角线AC上取点E,使得∠CDE=15°,连接BE.延长BE到F,连接CF,使得CF=BC.
(1)求证:DE=BE;
(2)求证:EF=CE+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)![]()
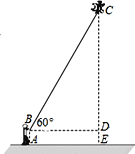
(2)如图,小方在清明假期中到郊外放风筝,风筝飞到C 处时的线长BC为20米,此时小方正好站在A处,并测得∠CBD=60°,牵引底端B离地面1.5米,求此时风筝离地面的高度.(![]() ,
,![]() ,结果精确到0.1米)
,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
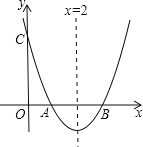
【题目】如图,已知抛物线![]() 与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)设P为对称轴上一动点,求△APC周长的最小值;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是红球的概率为![]() .
.
(1)布袋里红球有______个.
(2)先从布袋中摸出个球后不放回,再摸出1个球,请用列表或画树状图的方法求出两次摸到的球都是白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com