
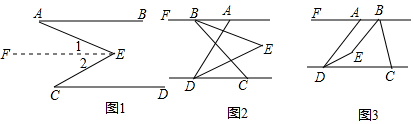
分析 (1)根据平行线的性质即可得到结论;
(2)先过点E作EH∥AB,根据平行线的性质和角平分线的定义,即可得到结论;
(3)过E作EG∥AB,根据平行线的性质和角平分线的定义,即可得到结论.
解答 解:阅读填空:
(1)平行于同一条直线的两条直线平行;
两直线平行,内错角相等;
等量代换,
故答案为:平行于同一条直线的两条直线平行,两直线平行,内错角相等,等量代换;
思维拓展:
(2)如图2,过点E作EH∥AB,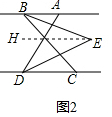
∵AB∥CD,∠FAD=m°,
∴∠FAD=∠ADC=m°,
∵DE平分∠ADC,∠ADC=m°,.
∴∠EDC=$\frac{1}{2}$∠ADC=$\frac{1}{2}$m°,
∵BE平分∠ABC,∠ABC=n°,
∴∠ABE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$n°,
∵AB∥CD,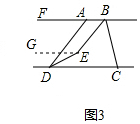
∴AB∥CD∥EH,
∴∠ABE=∠BEH=$\frac{1}{2}$n°,∠CDE=∠DEH=$\frac{1}{2}$m°,
∴∠BED=∠BEH+∠DEH=$\frac{1}{2}$n°+$\frac{1}{2}$m°=$\frac{1}{2}$( n°+m°);
(3)∠BED的度数改变.
过点E作EG∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=∠GAD=m°
∴∠ABE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$n°,∠CDE=$\frac{1}{2}$∠ADC=$\frac{1}{2}$m°
∵AB∥CD,
∴AB∥CD∥EG,
∴∠BEG=180°-∠ABE=180°-$\frac{1}{2}$n°,∠CDE=∠DEG=$\frac{1}{2}$m°,
∴∠BED=∠BEG+∠DEG=180°-$\frac{1}{2}$n°+$\frac{1}{2}$m°.
故答案为:180°-$\frac{1}{2}$n°+$\frac{1}{2}$m°.
点评 本题主要考查了平移的性质,平行线的性质以及角平分线的定义的运用,解决问题的关键是正确的作出辅助线.


科目:初中数学 来源: 题型:选择题
| A. | 4<m<5 | B. | 4≤m<5 | C. | 4<m≤5 | D. | 4≤m≤5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com