
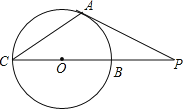
【题目】如图,PA切⊙O于点A,PC过点O且与⊙O交于B,C两点,若PA=6cm,PB=2![]() cm,则△PAC的面积是_____cm2.
cm,则△PAC的面积是_____cm2.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
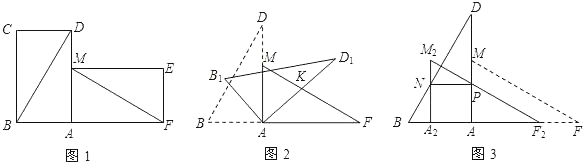
【题目】有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,∠ADB=30°.
(1)试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;
(2)把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1,边AD1交FM 于点K(如图2),设旋转角为β(0°<β<90°),当△AFK 为等腰三角形时,求β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,根据习俗每家每户都会在门口挂灯笼和对联,某商店看准了商机,购进了一批红灯笼和对联进行销售,已知每幅对联的进价比每个红灯笼的进价少10元,且用480元购进对联的幅数是用同样金额购进红灯笼个数的6倍.
(1)求每幅对联和每个红灯笼的进价分别是多少?
(2)由于销售火爆,第一批销售完了以后,该商店用相同的价格再购进300幅对联和200个红灯笼,已知对联售价为6元一幅,红灯笼售价为24元一个,销售一段时间后,对联卖出了总数的![]() ,红灯笼售出了总数的
,红灯笼售出了总数的![]() ,为了清仓,该店老板对剩下的对联和红灯笼以相同的折扣数进行打折销售,并很快全部售出,求商店最低打几折可以使得这批货的总利润率不低于90%?
,为了清仓,该店老板对剩下的对联和红灯笼以相同的折扣数进行打折销售,并很快全部售出,求商店最低打几折可以使得这批货的总利润率不低于90%?
查看答案和解析>>
科目:初中数学 来源: 题型:
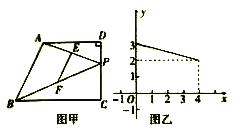
【题目】如图甲,在四边形ABCD中,AD//BC,∠C=90°动点P从点C出发沿线段CD向点D运动.到达点D即停止,若E、F分别是AP、BP的中点,设CP=x,△PEF的面积为y,且y与x之间的函数关系的图象如图乙所示,则线段AB长为( )
A.2![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着近几年城市建设的快速发展.某市对花木的需求量逐年提高,某园林专业户计划投资15万元种植花卉和树木.根据市场调查与预测,种植树木的利润y1(万元)与投资量x(万元)成正比例关系,如图①所示;种植花卉的利润y2(万元)与投资量x(万元)的函数关系如图②所示(其中OA是抛物线的一部分,A为抛物线的顶点;AB//x轴)。
(1)求出y1和y2关于投资量x的函数关系式
(2)求此专业户种植花卉和树木获取的总利润W(万元)关于投入种植花卉的资金t(万元)之间的函数关系式:
(3)此专业户投入种植花卉的资金为多少万元时,才能使获取的利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,进市场调查,甲种花卉的种植费用y(元)与种植面积xm2之间的函数关系如图所示,乙种花卉的种植费用为100元/m2.
(1)请直接写出当0≤x≤300和x>300时,y与x的函数关系式;

(2)广场上甲、乙两种花卉的种植面积共1200m2,如果甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
(3)在(2)的条件下,若种植总费用不小于123000元,求出甲种花卉种植面积的范围是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗. 我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店代理某品牌商品的销售.已知该品牌商品进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),付员工的工资每人每天100元,每天还应支付其它费用150元.
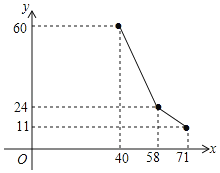
(1)求日销售y(件)与销售价x(元/件)之间的函数关系式;
(2)该店员工人共3人,若某天收支恰好平衡(收入=支出),求当天的销售价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com