
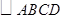 在平面直角坐标系中,
在平面直角坐标系中,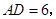 若
若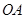 、
、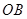 的长是关于
的长是关于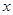 的一元二次方程
的一元二次方程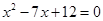 的两个根,且
的两个根,且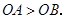
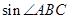 的值.
的值.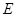 为
为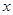 轴上的点,且
轴上的点,且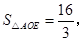 求经过
求经过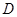 、
、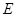 两点的直线的解析式,并判断
两点的直线的解析式,并判断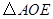 与
与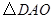 是否相似?
是否相似?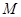 在平面直角坐标系内,则在直线
在平面直角坐标系内,则在直线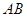 上是否存在点
上是否存在点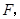 使以
使以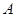 、
、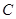 、
、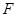 、
、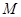 为顶点的四边形为菱形?若存在,请直接写出
为顶点的四边形为菱形?若存在,请直接写出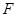 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.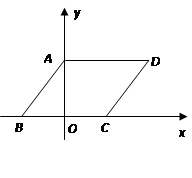
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源:不详 题型:解答题
 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
 = ,并结合图②证明你的猜想;(5分)
= ,并结合图②证明你的猜想;(5分) 的值.(用含α的式子表示)(5分)
的值.(用含α的式子表示)(5分) 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
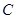 将线段
将线段 分成两部分,如果
分成两部分,如果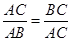 ,那么称点
,那么称点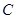 为线段
为线段 的黄金分割点.
的黄金分割点. 将一个面积为
将一个面积为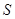 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为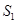 ,
,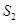 ,如果
,如果 ,那么称直线
,那么称直线 为该图形的黄金分割线.
为该图形的黄金分割线.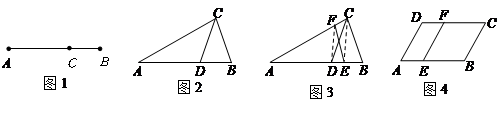
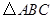 中,若点
中,若点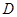 为
为 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线 是
是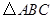 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?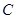 任作一条直线交
任作一条直线交 于点
于点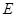 ,再过点
,再过点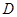 作直线
作直线 ,交
,交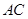 于点
于点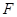 ,连接
,连接 (如图3),则直线
(如图3),则直线 也是
也是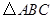 的黄金分割线.
的黄金分割线.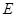 是
是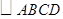 的边
的边 的黄金分割点,过点
的黄金分割点,过点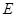 作
作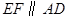 ,交
,交 于点
于点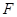 ,显然直线
,显然直线 是
是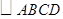 的黄金分割线.请你画一条
的黄金分割线.请你画一条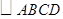 的黄金分割线,使它不经过
的黄金分割线,使它不经过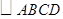 各边黄金分割点.
各边黄金分割点.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
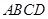 沿
沿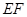 对开后,再把矩形
对开后,再把矩形 沿
沿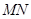 对开,依此类推.若各种开本的矩形都相似,那么
对开,依此类推.若各种开本的矩形都相似,那么 等于( ).
等于( ).
A. | B. | C.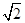 | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com